A small body of mass m slides down from the top of a hemisphere of radius r. The surface of block and hemisphere are frictionless. The height at which the body lose contact with the surface of the sphere is

(3/2)r
(2/3)r
(12)gr2
v2/2g
The correct Answer is:B
The body will lose constanct when centripetal acceleration becomes equal to the component of accelerationdue to gravity along the radius.

Velocity at P,v=√2g(r−h)(∴V2−u2=2gx)
Centripetal acceleration will v2/r. it should be equal to the component of g along PO. Hence.
v2r=gcosθor(2g(r−h)r=g×hr
Solving we get, h=(2r3)
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DISHA PUBLICATIONCHAPTER - LAWS OF MOTIONEXERCISE - Exercise-1: Concept Builder (Topicwise) (Topic 5: Circular Motion and Banking of Road )
7 Videos
- JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))BOOK - DISHA PUBLICATIONCHAPTER - JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))EXERCISE - QUESTIONS
30 Videos
- MAGNETISM AND MATTERBOOK - DISHA PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE-2:CONCEPT APPLICATOR
31 Videos
Similar Questions
A small block slides down from the top of hemisphere of radius R = 3 m as shown in the figure. The height 'h' at which the block will lose contact with the surface of the sphere is __________ m.
(Assume there is no friction between the block and the hemisphere)
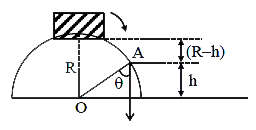
View SolutionA small body of mass m slides without friction from the top of a hemisphere of radius r. At what hight will the body be detached from the centre of hemisphere?

View Solution
Knowledge Check
The total surface area of a solid hemisphere of radius r is
Aπr2B2πr2C3πr2D4πr2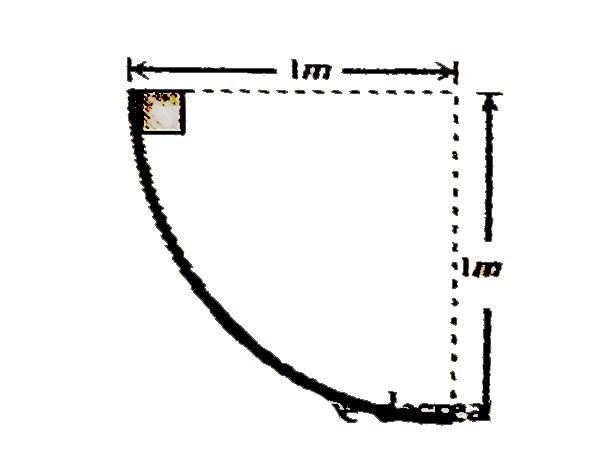
A body of mass 2kg slides down a curved track which is quadrant of a circle of radius 1 metre . All the surfaces are frictionless. If the body starts from rest, its speed at the bottom of the track isA4.43m/secB2m/secC0.5m/secD19.6m/ec
A small body of mass m slides without friction from the top of a hemisphere of radius r. At what hight will the body be detached from the surface of hemisphere?

View SolutionA particle of mass m is released from the top of a smooth hemisphere of radius R with the horizontal speed μ. Calculate the angle with verticle where it loses contact with the hemisphere.
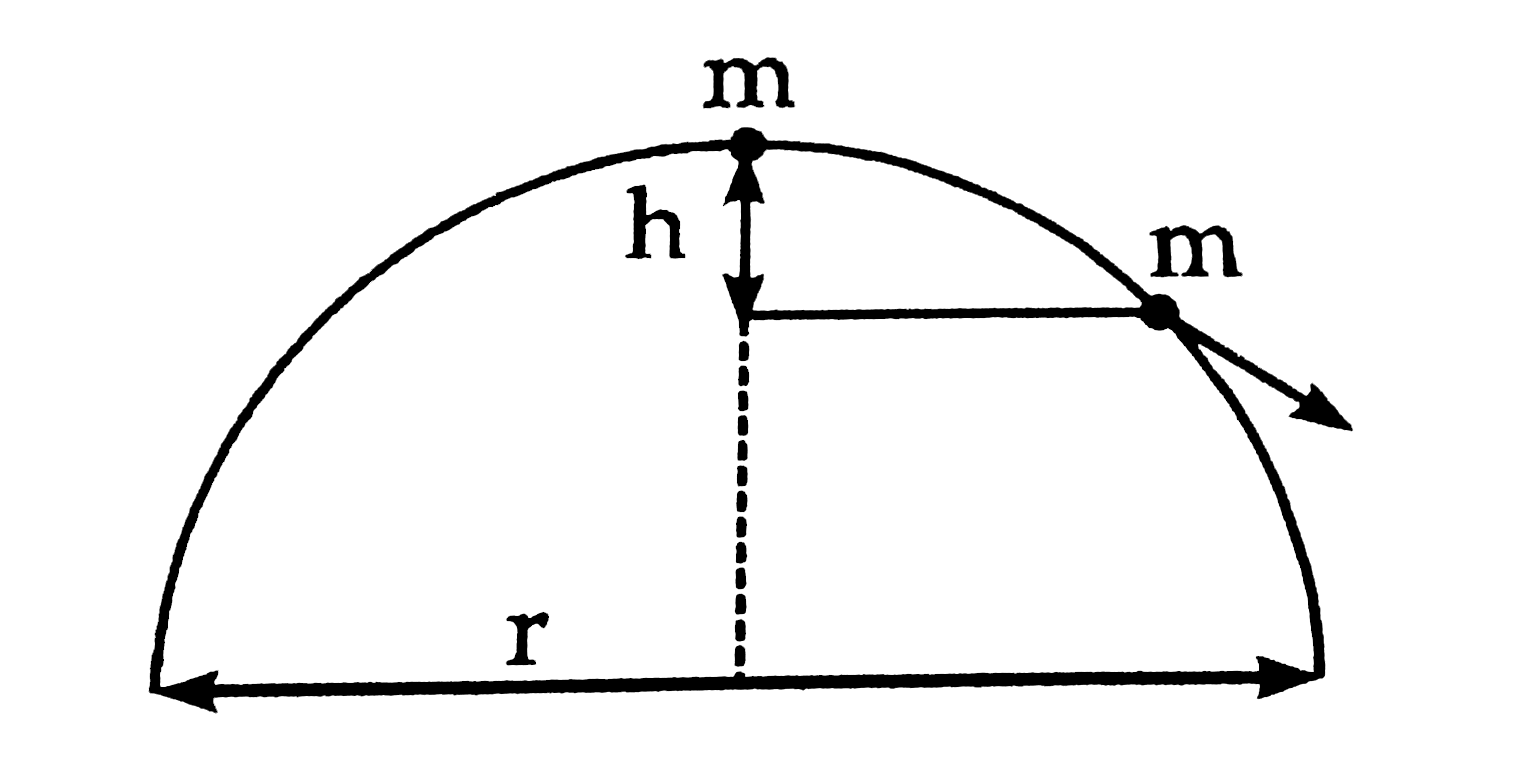
View SolutionA small block of mass m has speed√gR2 at the top most point of a fixed hemisphere of radius R as shown in figure. The angle θ, when block loses the contact with the hemisphere is
_PHY_E05_149_Q01.png)
View SolutionA small body of mass m slide without friction from the top of a hemispherical cup of radius r as shown in figure. If leaves the surface to the cup at vertial distance h below the highest point then
View SolutionWhat is the total surface area of hemisphere if the radius of hemisphere is r.
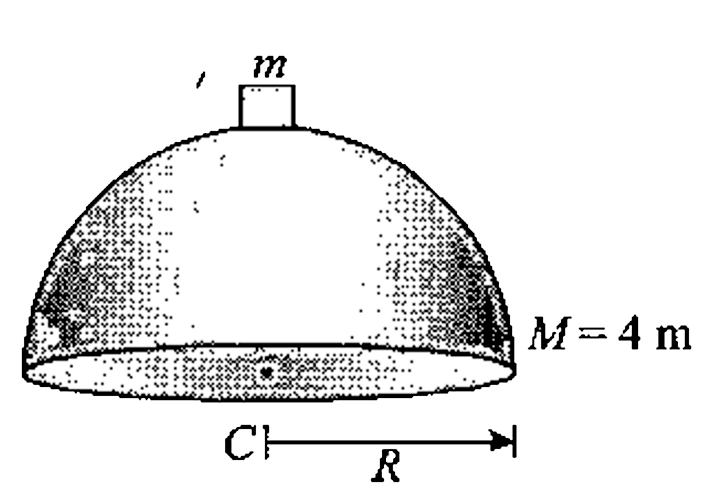
View SolutionA small block of mass m starts sliding down from rest along the smooth surface of a fixed hollow hemisphere of same mass m. Find the distance of centre of mass of block and hemishere from centre of hemisphere C when block m separates from the surface of hemisphere.
View Solution
