An insect crawls up a hemispherical surface very slowly. The coefficient of friction between the insect and the surface is 1/3. If the line joining the centre of the hemispherical surface to the insect makes an angle a with the vertical, the maximum possible value of α so that the insect does not slip is given by

cotα=3
secα=3
cosecα3
cosα=3
The correct Answer is:A
The insect crawls up the bowl upto a certain height h only till the component of its weight along the bowl is balanced by limiting frictional force.
Force limiting condition at point A
R−mgcosα ...(i)
F1=mgsinα ...(ii)
Dividing eq. (ii) by (i)
tanα=1cotα=F1R=μ[AsF1=μR]
⇒tanα=μ=13[∴μ=13 (given)]

Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DISHA PUBLICATIONCHAPTER - LAWS OF MOTIONEXERCISE - Exercise-1: Concept Builder (Topicwise) (Topic 5: Circular Motion and Banking of Road )
7 Videos
- JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))BOOK - DISHA PUBLICATIONCHAPTER - JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))EXERCISE - QUESTIONS
30 Videos
- MAGNETISM AND MATTERBOOK - DISHA PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE-2:CONCEPT APPLICATOR
31 Videos
Similar Questions
An insect craws up a hemispherical surface very slowly (see fig.). The coefficient of friction between the insect and the surface is 1/3. If the line joining the center of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by

View SolutionAn insect craws up a hemispherical surface very slowly (see fig.). The coefficient of friction between the insect and the surface is 1/3. If the line joining the center of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by

View Solution
Knowledge Check
An insect crawls up a hemispherical surface very slowly (see the figure). The coefficient of friction between the insect and the surface is 1/3. If the line joining the centre of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by
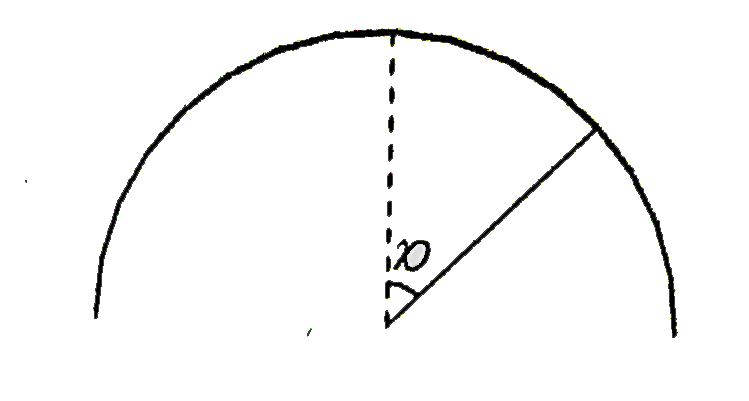 Acotα=3Btanα=3Csecα=3Dcosecα=3
Acotα=3Btanα=3Csecα=3Dcosecα=3An insect craws up a hemispherical surface very slowly (see fig.). The coefficient of friction between the insect and the surface is 1/3. If the line joining the center of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by
 Acotα=3Btanα=3Csecα=3Dcosecα=3
Acotα=3Btanα=3Csecα=3Dcosecα=3
An insect craws up a hemispherical surface very slowly (see fig.). The coefficient of friction between the insect and the surface is 1/3. If the line joining the center of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by

View SolutionAn insect crawls up a hemispherical surface very slowly. The coefficient of friction between the insect and the surface is 1/3. If the line joining the centre of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of is given by:
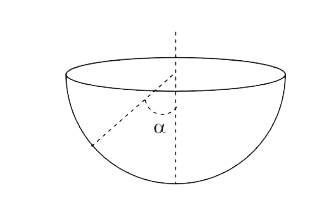
View SolutionIf the coefficient of friction between an insect and bowl is μ and the radius of the bowl is r, find the maximum height to which the insect can crawl in the bowl.
View SolutionIf the coefficient of friction between an insect and bowl is μ and the radius of the bowl is r, find the maximum height to which the insect can crawl in the bowl.
View SolutionIf the coefficient of friction between an insect and bowl is μ and the radius of the bowl is r, find the maximum height to which the insect can crawl in the bowl.
View SolutionIf the coefficient of friction between an insect and bowl is μ and the radius of the bowl is r, find the maximum height to which the insect can crawl in the bowl.
View Solution
