A palne is inclined at an angle α=30∘ with respect to the horizontal. A particle is projected with a speed u=2ms−1 from the base of the plane, as shown in figure. The distance (in metre) from the base, at which the particle hits the plane is close to: (Take g=10ms−2)

On an inclined plane, time fo flight (T) is given by
T=2usinθgcosα
Substituting the value we get
T=(2)(2sin15∘)gcos30∘=4sin15∘10cos30∘
Distance S=(2cos15∘)T−12gsin30∘(T)2

=(2cos15∘)410sin15∘10cos30∘−(12×10sin30∘)16sin215∘100cos230∘
=16√3−1660=0.195m
Topper's Solved these Questions
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER -4 (LAWS OF MOTION)
15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER -5 (WORK, ENERGY AND POWER)
15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER -2 (Motion in a Straight Line)
15 Videos
- ATOMSBOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-2: CONCEPT APPLICATOR
30 Videos
- COMMUNICATION SYSTEM BOOK - DISHA PUBLICATIONCHAPTER - COMMUNICATION SYSTEM EXERCISE - EXERCISE-2 : Concept Applicator
30 Videos
Similar Questions
A particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View Solution
Knowledge Check
A ball is projected from point A with velocity 10ms−1 perpendicular to the inclined plane as shown in figure. Range of the ball on the inclined plane is
 A403mB2013mC1320mD1340m
A403mB2013mC1320mD1340mA particle is projected at an angle θ=30∘ with the horizontal, with a velocity of 10ms−1. Then
AAfter 2 s, the velocity of particle makes an angle of 60∘ with initial velocity vector.BAfter 1 s, the velocity of particles makes an angle of 60∘ with initial velocity vector.CThe magnitude of velocity of particle after 1 s is 10ms−1.DThe magnitude of velocity of particle after 1 s is 5ms−1.
A particle is projected horizontal with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane?
View SolutionAn inclined plane makes an angle θ0=30∘ with the horizontal. A particle is projected from this plane with a speed of 5ms−1 at an angle of elevation β=30∘ with the horizontal as shown in (Fig. 5.53).
(a) Find the range of the particle on the plane when it strikes the plane.
(b) Find the range of the particle for β=120∘.
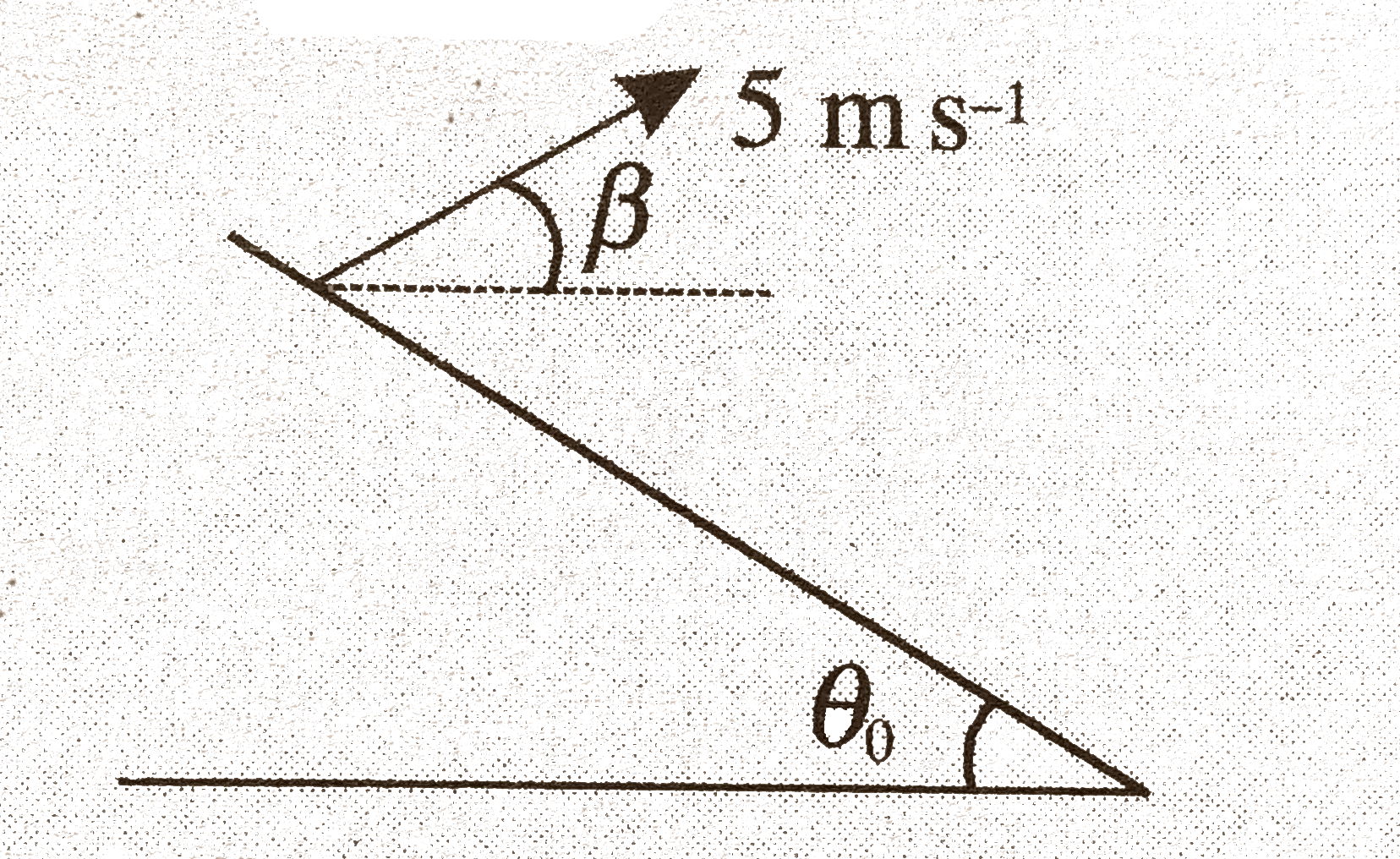 .
.
View SolutionAn inclined plane makes an angle θ0=30∘ with the horizontal. A particle is projected from this plane with a speed of 5ms−1 at an angle of elevation β=30∘ with the horizontal as shown in (Fig. 5.53).
(a) Find the range of the particle on the plane when it strikes the plane.
(b) Find the range of the particle for β=120∘.
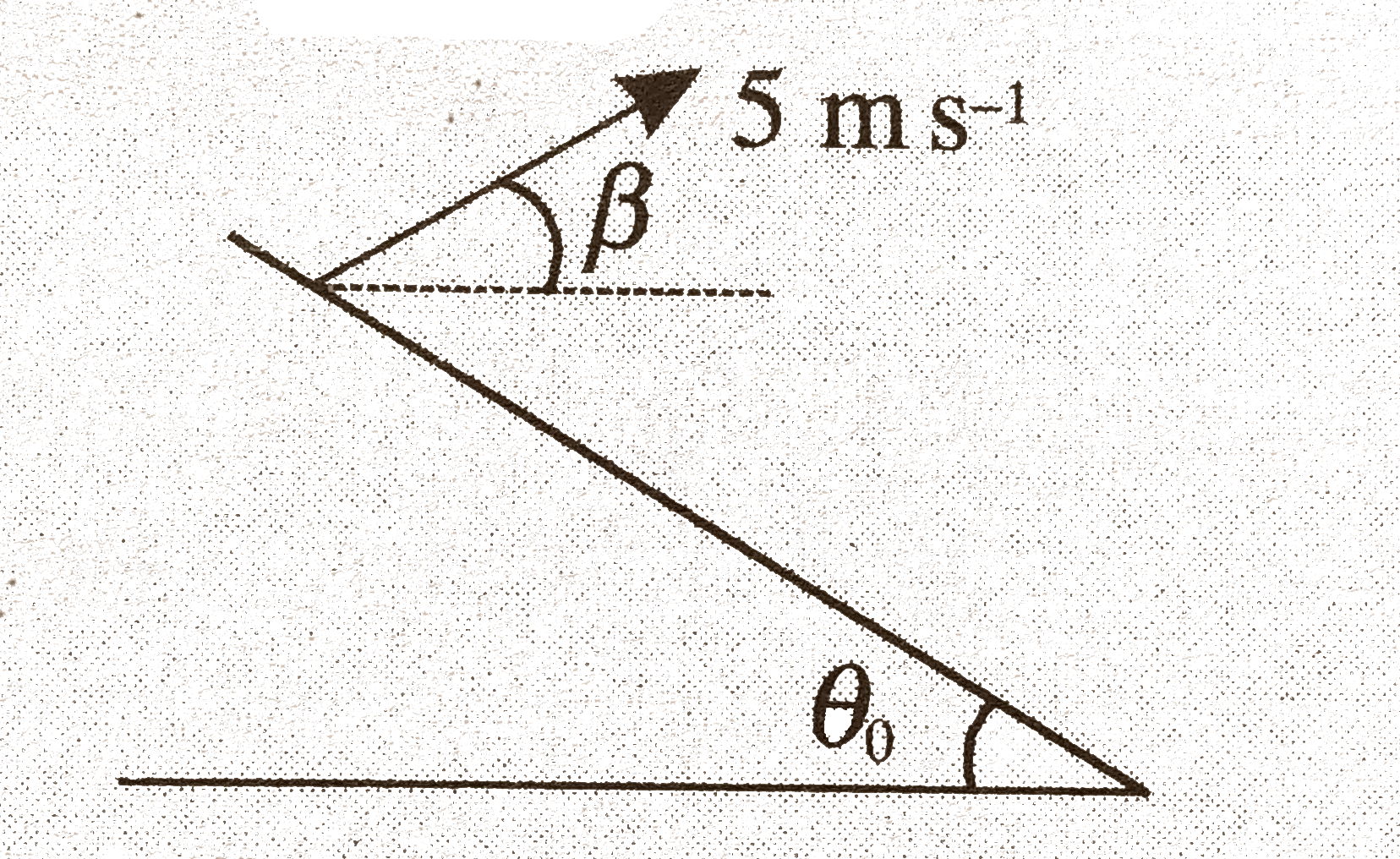 .
.
View SolutionA particle is projected from the ground and simultaneously a wedge starts moving towards the right, as shown in the figure. The maximum height of the wedge for which the particle will not hit the wedge is [g=10ms−2]
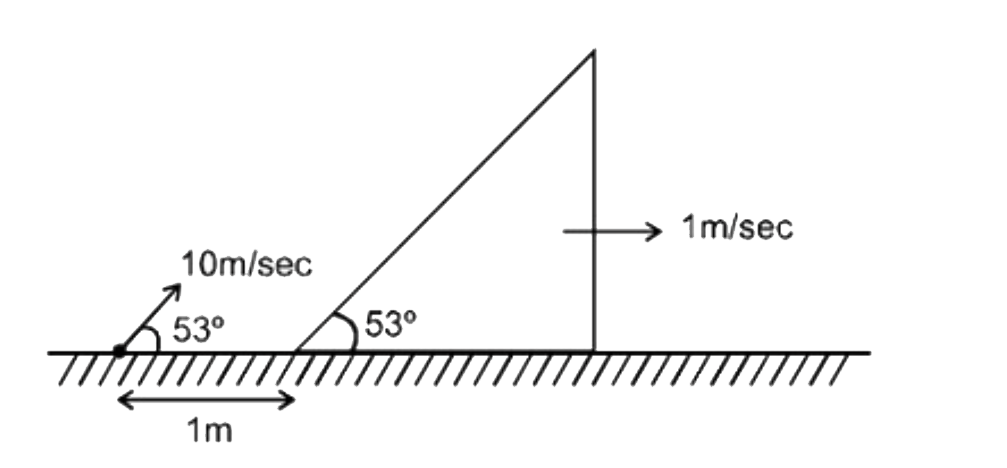
View SolutionA particle is projected from the ground and simultaneously a wedge starts moving towards the right, as shown in the figure. The maximum height of the wedge for which the particle will not hit the wedge is [g=10ms−2]

View SolutionA particle is projected at an angle θ=30∘ with the horizontal, with a velocity of 10ms−1. Then
View Solution
