A wooden plank of length 1 m and uniform cross section is hinged at one end to the bottom of a tank as shown in Figure. The tank is filled with water up to a height of 0.5 m. The specific gravity of the plank is 0.5. Find the angle (in degree) that the plank makes the vertical in the equilibrium position (Exclude the case $θ = 0$ ).

Text Solution

Verified by Experts

Let y is the length of the plank inside water
$∴ y = \frac{0.5}{cos θ}$

Let A be the cross sectional area of the plank then buoyant force on it
$F_{b} = V ρ_{u} g$
$= (A y) ρ_{w} g$
Since plank is in rotational equilibrium, so
$\sum {¯ τ}_{0} = 0$

or $m g \times \frac{l}{2} sin θ - F_{b} \times \frac{y}{2} sin θ = 0$
or $m g l - F_{b} \times y = 0$
$(A l \times 0.5) g l - (A y) d_{w} y = 0$
or $0.5 l^{2} = y^{2}$
or $0.5 \times {(1)}^{2} = {(\frac{0.5}{cos θ})}^{2}$
$\Rightarrow {cos}^{2} θ = \frac{1}{2}$
or $cos θ = \frac{1}{\sqrt{2}}$
or $θ = 45^{\circ}$

Updated on:21/07/2023

A wooden rod of a uniform cross section and of length $120 c m$ is hinged at the bottom of the tank which is filled with water to a height of $40 c m$ . In the equilibrium position, the rod makes an angle of $60^{\circ}$ with the vertical. The centre of buoyancy is located on the rod at a distance (from the hinge) of
A $20 c m$
B $40 c m$
C $60 c m$
D $75 c m$
A uniform rod of length 2.0 m specific gravity 0.5 and mass 2 kg is hinged at one end to the bottom of a tank of water (specific gravity = 10) filled upto a height o f 1.0 m as shown in figure. Taking the case $θ = - 0^{\circ}$ the force exerted by the hings on the rod is $(g = 10 m / s^{2})$

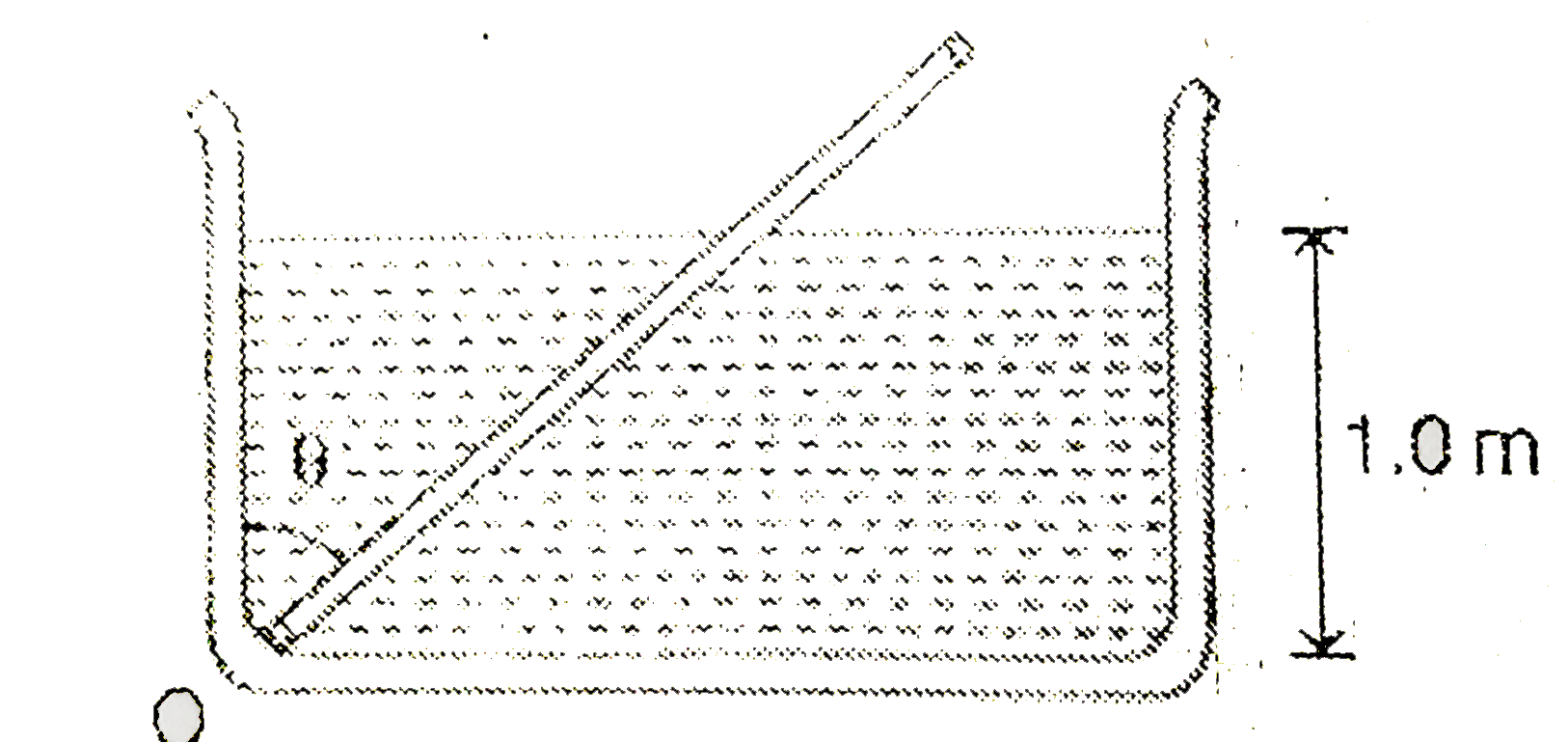A10.2 N upwards
B4.2 N downwards
C8.3 N downwards
D6.2 N upwards