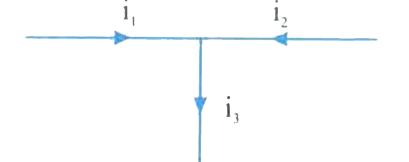
If $i_{1} = 3 \sin ω t, i_{2} = 4 \cos ω t$ , and $i_{3} = i_{0} \sin (ω t + 53^{\circ})$ find the value of $i_{0}$ .

Text Solution

Verified by Experts

From Kirchoff.s current law
$i_{3} = i_{1} = i_{2} = 3 \sin ω t + 4 \sin (ω t + 90^{\circ})$
$\Rightarrow i_{3} = i_{0} \sin (ω t + ϕ)$
where $i_{0} = \sqrt{3^{2} + 4^{2} + 2 (3) (4) {\cos 90}^{\circ}}$
and $\tan ϕ = \frac{4 {\sin 90}^{\circ}}{3 + 4 {\cos 90}^{\circ}} = \frac{4}{3}$
$∴ i_{3} = 5 \sin (ω t + 53^{\circ})$

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

If $i_{1} = 3 sin ω t and (i_{2}) = 4 cos ω t,$ then $(i_{3})$ is

A $5 sin (ω t + 53^{\circ})$
B $5 sin (ω t + 37^{\circ})$
C $5 sin (ω t + 45^{\circ})$
D $5 sin (ω t + 35^{\circ})$
If $i_{1} = i_{0} sin (ω t), i_{2} = i_{0_{2}} sin (ω t + ϕ)$ , then $i_{3} =$

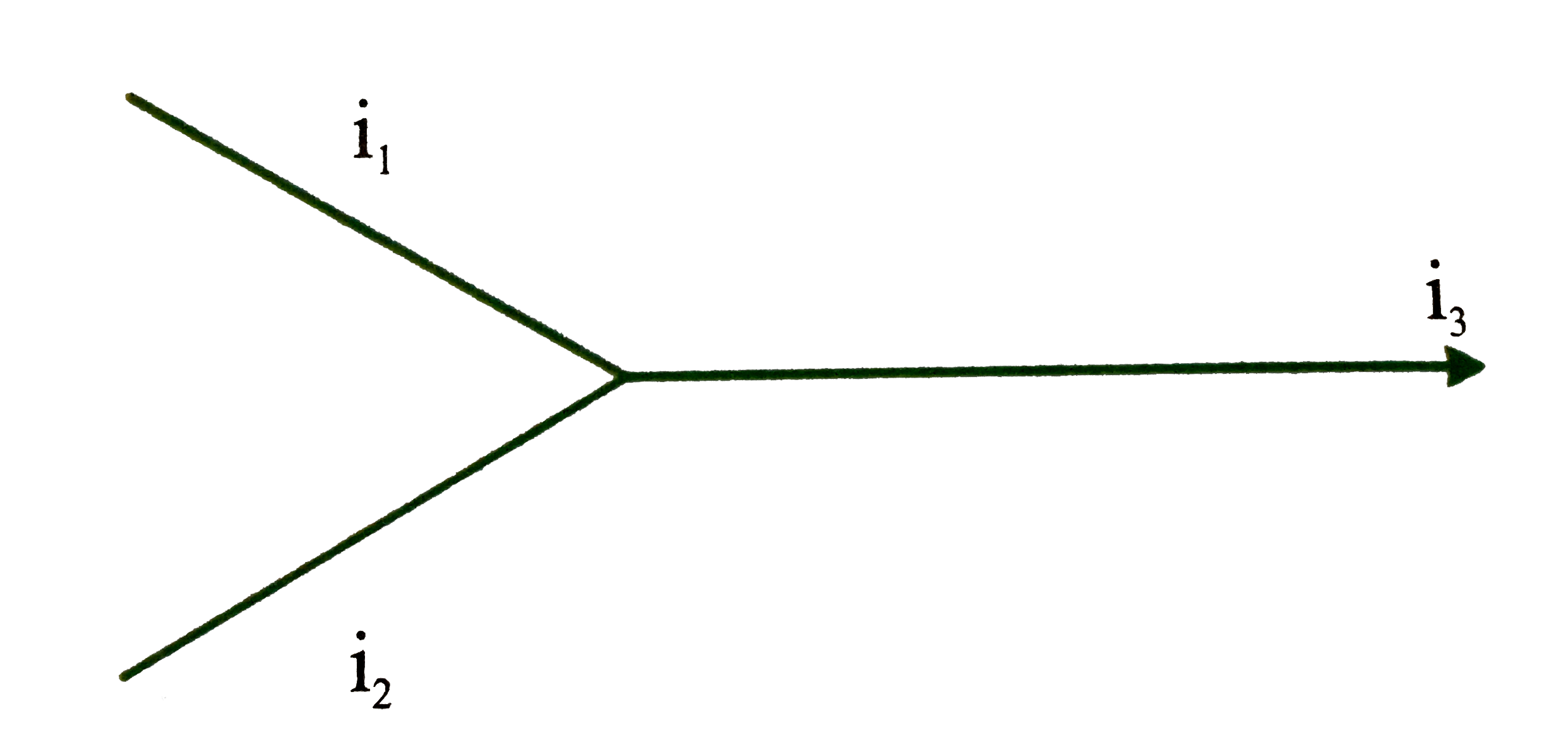A $\sqrt{i_{0_{1}}^{2} + i_{0_{2}}^{2}} sin {ϕ + ω t}$
B $(i_{0_{1}} + i_{0_{2}}) sin (\frac{ϕ}{2} + ω t)$
C $(\sqrt{i_{0_{1}}^{2} + i_{0_{2}}^{2} + 2 i_{0_{1}} i_{0_{2}} cos ϕ}) sin [ϕ + ω t]$
D $(\sqrt{i_{0_{1}}^{2} + i_{0_{2}}^{2} + 2 i_{0_{1}} i_{0_{2}} cos ϕ}) sin [α + ω t]$ where $α = {Tan}^{- 1} [\frac{i_{0_{2}} sin ϕ}{i_{0_{1}} + i_{0_{2}} cos ϕ}]$

DISHA PUBLICATION-CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONS-CHAPTER -21 : (ALTERNATING CURRENT)

Home
Ask Doubt
Profile