Given LCR circuit has L=5H,C=80μF,R=40Ω and variable frequency source of 200V. The source frequency (in Hz) which drives the circuit at resonance is xπ.Find the value of

f=12π√LC=22π√5×80×10−6=25πHz
Topper's Solved these Questions
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 22 : (ELECTROMAGNETIC WAVES)
15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 23 : (RAY OPTICS AND OPTICAL INSTRUMENTS)
15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 20 : (ELECTROMAGNETIC INDUCTION)
15 Videos
- ATOMSBOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-2: CONCEPT APPLICATOR
30 Videos
- COMMUNICATION SYSTEM BOOK - DISHA PUBLICATIONCHAPTER - COMMUNICATION SYSTEM EXERCISE - EXERCISE-2 : Concept Applicator
30 Videos
Similar Questions
A series LCR circuit with L=80mH,C=50μF and R=60ohm is connected to a variable frequency 220 V source. Determine (i) the source frequency which drives the circuitin resonance (iii) the quality factor Q of the circuit.
View SolutionFig. shows series LCR circuit with L=5.0H,C=80μF,R=40Ω connected to a variable frequency 240 V source. Calculate
(i) the angular frequency of the source which drives the circuit at resonance.
(ii) Current at the resonating frequency.
(iii) the rms pot. drop across the capacitor at resonance.
View Solution
Knowledge Check
Figure shows a series LCR circuit connected to a variable frequency 230 V source.

The source frequency which drives the circuit the circuit in resonance isA4 HzB5 HzC6 HzD8 HzFigure shows a series LCR circuit connected to a variable frequency 230 V source.

The source frequency which drives the circuit the circuit in resonance isA4 HzB5 HzC6 HzD8 Hz
Fig. shows series LCR circuit with L=5.0H,C=80μF,R=40Ω connected to a variable frequency 240 V source. Calculate
(i) the angular freuquency of the source which drives the circuit at resonance.
(ii) Current at the resonanting frequency.
(iii) the rms pot. drop across the capacitor at resonance.

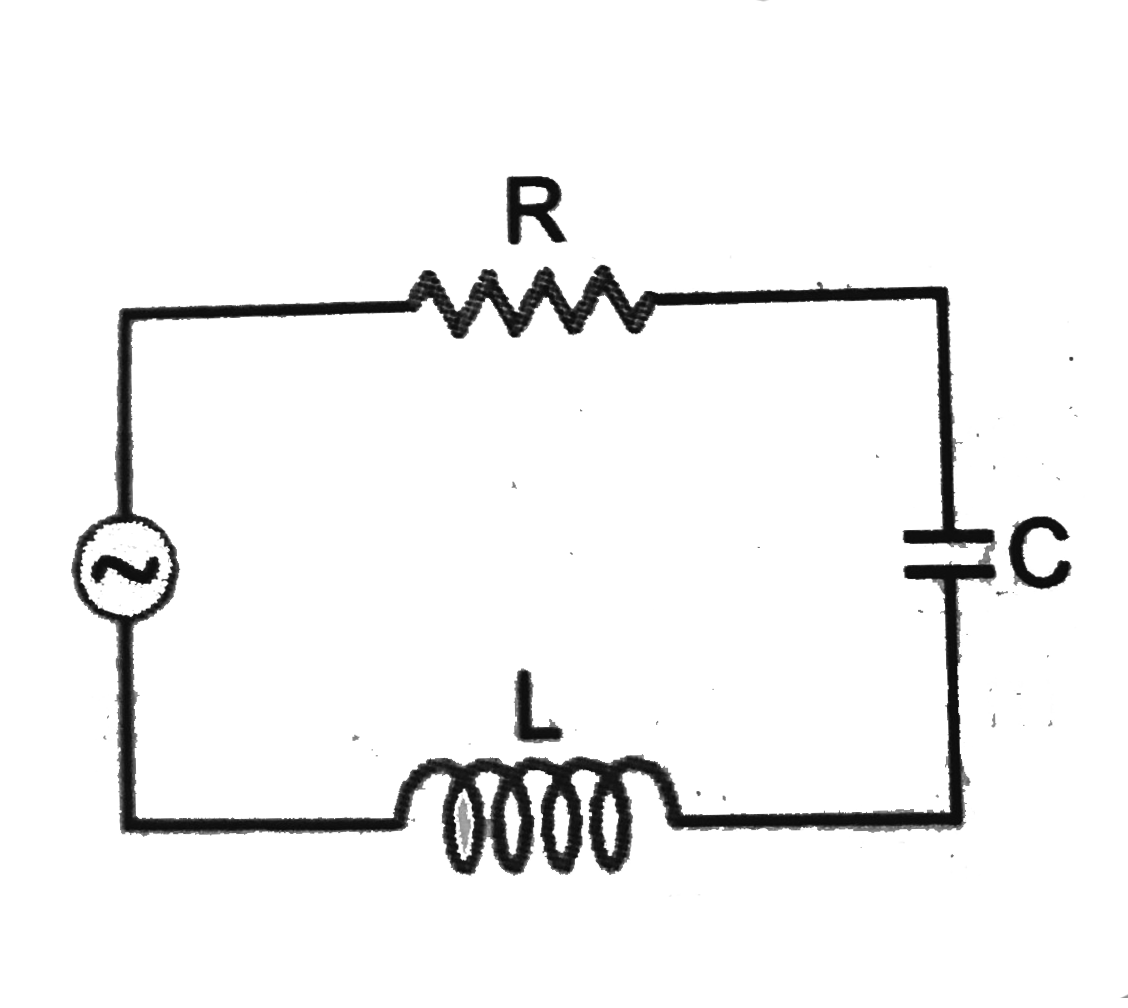
View SolutionA series LCR circuit connected to a variable frequency 230 V source has L = 5.0 H, C=80μF, R=40Ω, Fig.
(a) Determine the source frequency which drives the circuit in resonance.
(b) Obtain the impedance of the circuit and amplitude of current at at resonating frequency.
(c ) Determine the r.m.s. potential drops acorss the three elements the circuits. Show that the potential drop acorss the LC combination is zero at the resonating frequecny.
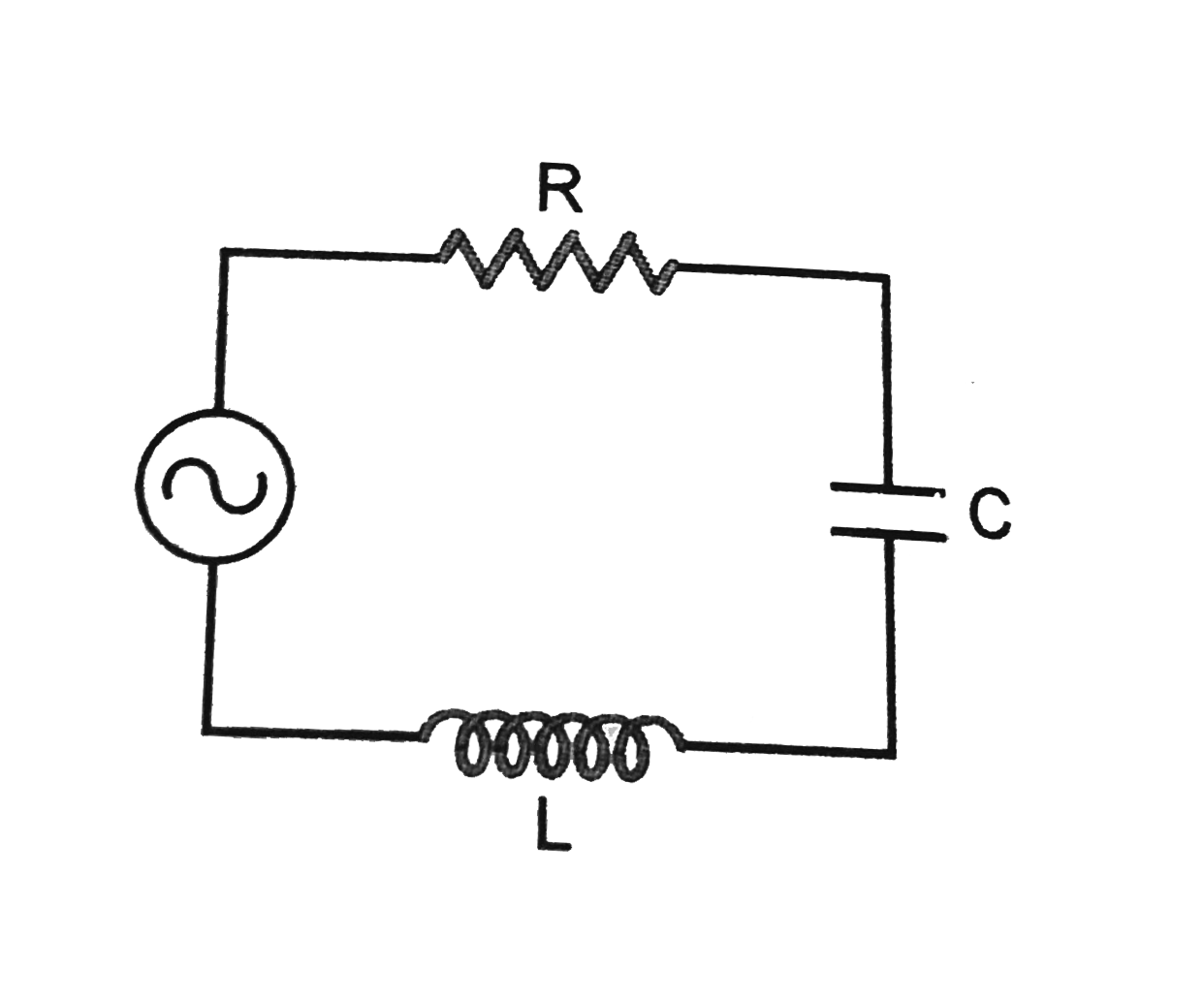
View SolutionA series LCR circuit connected to a variable frequency 230 V source has L = 5.0 H, C=80μF, R=40Ω, Fig.
(a) Determine the source frequency which drives the circuit in resonance.
(b) Obtain the impedance of the circuit and amplitude of current at at resonating frequency.
(c ) Determine the r.m.s. potential drops acorss the three elements the circuits. Show that the potential drop acorss the LC combination is zero at the resonating frequecny.

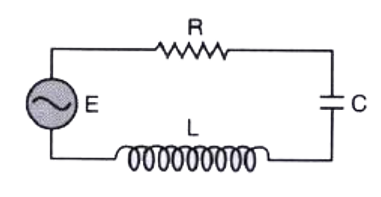
View SolutionThe figure shows a series LCR circuit connected to a varriable of 200 V source with L=50 mH, C=80μF and R=40Ω find.
(i) the source frequency which drives the circuit in resonance,
(ii) the quality factor (Q) of the circuit.
View SolutionA series LCR circuit with L=4.0H,C=100μF and R=60Ω is connected to a variable frequency 240 V source. Calculate
(i) angular frequency of the source which drives the circuit in resonance,
(ii) current at the resonating frequency,
(iii) rms potential drop across the inductance at resonance.
View SolutionFigure here, shows a series L-C-R circuit connected to a variable frequency 230 V source. L = 5.0H, C = 80μF and r =40Ω
(a) Determine the source frequency which drives the circuit in resonance.
(b) Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
(c) Determine the rms potential drops across the three elements of the circuit. show that the potential drop across the L-C combination is zero at the resonating frequency.

View Solution
