Question

What is the moment of inertia of a disc about one of its diameters?

Explanation

We assume the moment of inertia of the disc about an axis perpendicular to it and through its centre to be known, it is `MR^(2)//2`, where M is the mass of the disc and R is its radius (Table 7.1)
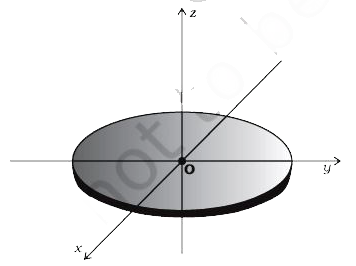
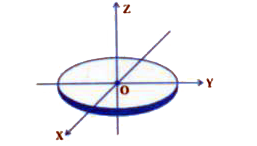
The disc can be considered to be a planar body. Hence the theorem of perpendicular axes is applicable to it. As shown in Fig. 7.30, we take three concurrent axes through the centre of the disc, O, as the `x–, y– and z–`axes, `x– and y–`axes lie in the plane of the disc and z–axis is perpendicular to it. By the theorem of perpendicular axes,
`I_(z)=I_(x)+I_(y)`
Now, x and y axes are along two diameters of the disc, and by symmetry the moment of inertia of the disc is the same about any diameter. Hence
`I_(x)=I_(y)`
and `I_(z)=2I_(x)`
But `I_(z)=MR^(2)//2`
So finally, `I_(x)=I_(z)//2=MR^(2)//4`
Thus the moment of inertia of a disc about any of its diameter is `MR^(2)//4`.
Find similarly the moment of inertia of a ring about any of its diameters. Will the theorem be applicable to a solid cylinder?