What is the moment of inertia of a disc about one of its diameters?
Text Solution
We assume the moment of inertia of the disc about an axis perpendicular to it and through its centre to be known, it is , where M is the mass of the disc and R is its radius (Table 7.1)
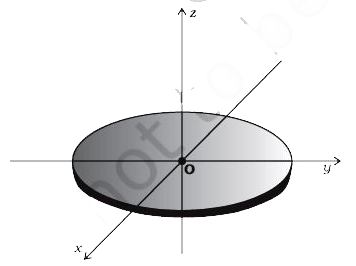
The disc can be considered to be a planar body. Hence the theorem of perpendicular axes is applicable to it. As shown in Fig. 7.30, we take three concurrent axes through the centre of the disc, O, as the axes, axes lie in the plane of the disc and z–axis is perpendicular to it. By the theorem of perpendicular axes,
Now, x and y axes are along two diameters of the disc, and by symmetry the moment of inertia of the disc is the same about any diameter. Hence
and
But
So finally,
Thus the moment of inertia of a disc about any of its diameter is .
Find similarly the moment of inertia of a ring about any of its diameters. Will the theorem be applicable to a solid cylinder?
|
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - NCERT BANGLISHCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISES
26 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - NCERT BANGLISHCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISES (TRUE OR FALSE)
3 Videos
- OSCILLATIONSBOOK - NCERT BANGLISHCHAPTER - OSCILLATIONSEXERCISE - Additional Exercises
6 Videos
- THERMAL PROPERTIME OF MATTERBOOK - NCERT BANGLISHCHAPTER - THERMAL PROPERTIME OF MATTEREXERCISE - EXERCISES
30 Videos
Similar Questions
Knowledge Check
The moment of inertia of a circular dics about one of its diameters is l. What will be its moment of inertia about a tangent parallel to the diameter?
A4lB2lC5l2D5lThe moment of inertia of a ring about one of its diameter is 2kgm2 . What will be its moment of inertia about a tangent parallel to the diameter?
A2kgm2B6kgm2C4khm2D5kgm2The moment of inertia of a circular ring about one of its diameters is I . What will be its moment of inertia about a tangent parallel to the diameter?
A4 IB2 IC32ID3I
Calculate the moment of inertia of a disc about its any diameter ?
View SolutionCalculate the moment of inertia of a disc about its any diameter ?
View SolutionCalculate the moment of inertia of a disc about its any diameter ?
View SolutionThe moment of inertia of a ring about one of its diameters is I.What willbe its moment of inertia about a tangent parallel to the diameter ?
View SolutionThe moment of inertia of a ring about one of its diameters is I.What willbe its moment of inertia about a tangent parallel to the diameter ?
View Solution
