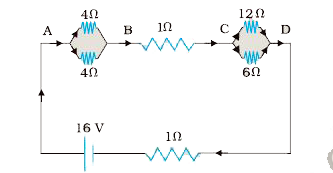
A network of resistore is connected to a 16 V battery with internal resistance of 1Ω, as shown in (a) Compute the equivalent resistance of the network. (b) Obtain the current in each resistor. (c ) obtain the voltage drops VAB,VBCandVCD
 Solution in Telugu
Solution in Telugu
(a) The network is a simple series and parallel combination of resistors. First the two 4Ω resistors in parallel are equivalent to a resistor =[(4×4)/(4+4)Ome>a=2α
In the same way. The 12Ωand6Ω resistores in parallel are equivalent ot a resistor of
[(12×6)/(12+6)]Ω=4Ω
The equivalent resistance R of the networn is obtained by conmbining these resistore (2Ωand4Ω) with 1Ω in series. that is.
R=2Ω+4Ω+1Ω=7Ω
(b) The total current In in the circuit is
I=∈R+r=16v(7+1)Ω=2A
Consider the restors between A and B. If I1 is the current in one of the 4Ω resistors and I(2) the current in the other.
I1×4=I2×4
then is, I1=I2, which is otherwise obvious from the symmetry of the two arma. But I1+I2=I=2A. Thus.
I1=I2=1A
that , is current in each 4Ω resistor is 1A. Current in 1Ω resistor between B and C would be 2 A.
Now, consider the resistance between C and D. If I3 is the current in the 12Ω resistor, and I4 in the 6Ω rsistor.
I3×12=I4×6,i.e.,I4=2I3
But, I3+I4=I=2A
Thus, I3=(23)A,I4=(43)A
that is, the current in the 12Ω resistor is (2/3) A, whithe the current in the 6Ω resistor is (4/3) is
VAB=IA×4=1A×4Ω=4V.
This can also be obtained by multtplying the total current between A and B by the equivalent resistance between A and B, that is.
VAB=2A×2Ω=4V
The voltage drop across BC is
VBC=2A×1Ω=2V
Finally, the voltage drop across CD is
VCD=12Ω×I3=12Ω×(23)A=8V.
This can alternately be obtained by multiplying total current between C and D by the equivalent resistance between C and D. that is
VCD=2A×4Ω=8V
Note that the total voltage drop across AD is 4V+2V+8V=14V. Thus, the terminal voltage of the bettery is 14 V, while its emf is 16 V. The loss of the voltege (=2V) is accounted for by the internal resistance 1Ω of the bettery [2A×1Ω=2V].
Similar Questions
चित्र में दिखाए गए अनुसार आंतरिक 1Ω प्रतिरोध के की एक बैटरी में प्रतिरोधों के 16 V एक नेटवर्क को जोड़ा गया है
नेटवर्क का तुल्य प्रतिरोध परिकलित कीजिये |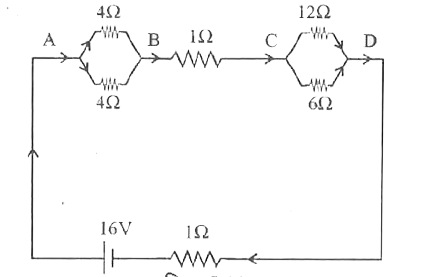 02:26View Solution
02:26View SolutionA network of resistors is connected to a 5 V battery with internal resistance of 1Omega as shown in Fig. (a) Compute the equivalent resistance of the network. (6) Obtain the current in each resistor. (c) Obtain the voltage drops V_(BC) and V_(CD)
04:42View SolutionA network of resistore is connected to a 16 V battery with internal resistance of 1Ω, as shown in (a) Compute the equivalent resistance of the network. (b) Obtain the current in each resistor. (c ) obtain the voltage drops VAB,VBCandVCD
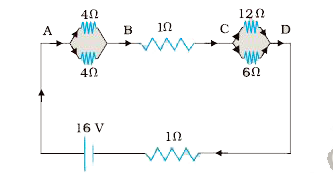 08:54View Solution
08:54View SolutionA network of resistances is connected to a 16 V battery with internal resistance of 1 Omega , as shown in Fig. 4.33. (a) Compute epuivalent resistance of the network, (b) obtain the current In in each resistor, and (c ) obtain the voltage drops V_(AB), V_(BC) " and " V_(CD) .
10:17View SolutionA network of resistore is connected to a 16 V battery with internal resistance of 1Ω, as shown in (a) Compute the equivalent resistance of the network. (b) Obtain the current in each resistor. (c ) obtain the voltage drops VAB,VBCandVCD
 08:54View Solution
08:54View SolutionAs shown in following figure, one network is connected to a battery of 16 V emf and internal resistance 1 Omega . Find (a) equivalent resistance of network. (b) current through each resistance. (c) voltage drops of V_(AB), V_(BC) , V_(CD) ,
03:33View SolutionA network of Resistors is Connected to a 16V battery with internal resistance 1Omega as shown in Figure below. (a) Compute the equivalent resistance of the network (b) Calculate the total current in the circuit
05:12View Solution

