Prove that : (i) adj I=I (ii) adj O=O (iii) I−1=I.
Step by step video & image solution for Prove that : (i) " adj " I=I (ii) " adj " O=O (iii) I^(-1)=I. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Prove that :
adj.In=In
View SolutionProve that :
adj.O=O
View SolutionProve that (adj. A)−1=(adj. A−1).
View SolutionIf A = =⎡⎢⎣−1111−1111−1⎤⎥⎦ find the values of
(i) |A||adj A| (ii) |adj (adj (adjA))|
(iii) |adj(3A)| (iv) adj adj A
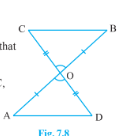
View SolutionIn Fig. 7.8, OA = OBand OD = OC. Show that (i)ΔAOD≅ΔBOC and (ii)AD ∣∣ BC.
View SolutionEvaluate: (i) i−50 (ii) i−9 (iii) i−131
View SolutionArrange the following in order of increasing radii ? (i) I, I+,I−(ii)C,N,Si,P(iii)O2,N3−,S2−,F−
View SolutionLet A=⎡⎢⎣1−21−231115⎤⎥⎦. Verify that ltbtgt (i) [adjA]−1=adj(A−1)
(ii) (A−1^(−1)=A
View SolutionEvaluate :
(i)i23 (ii)i998 (iii)i−998 (iv)i−71
(v)(√−1)91 (vi)(i37×i−61) (vii)i−1
View SolutionIn the given figure, O is the centre of the circle and OLM is perpendicular to AOB prove that (i) A, O, P and M are concyclic (i) ∠OAP=∠OMB (iii) P, L, O and B are concyclic
View Solution
