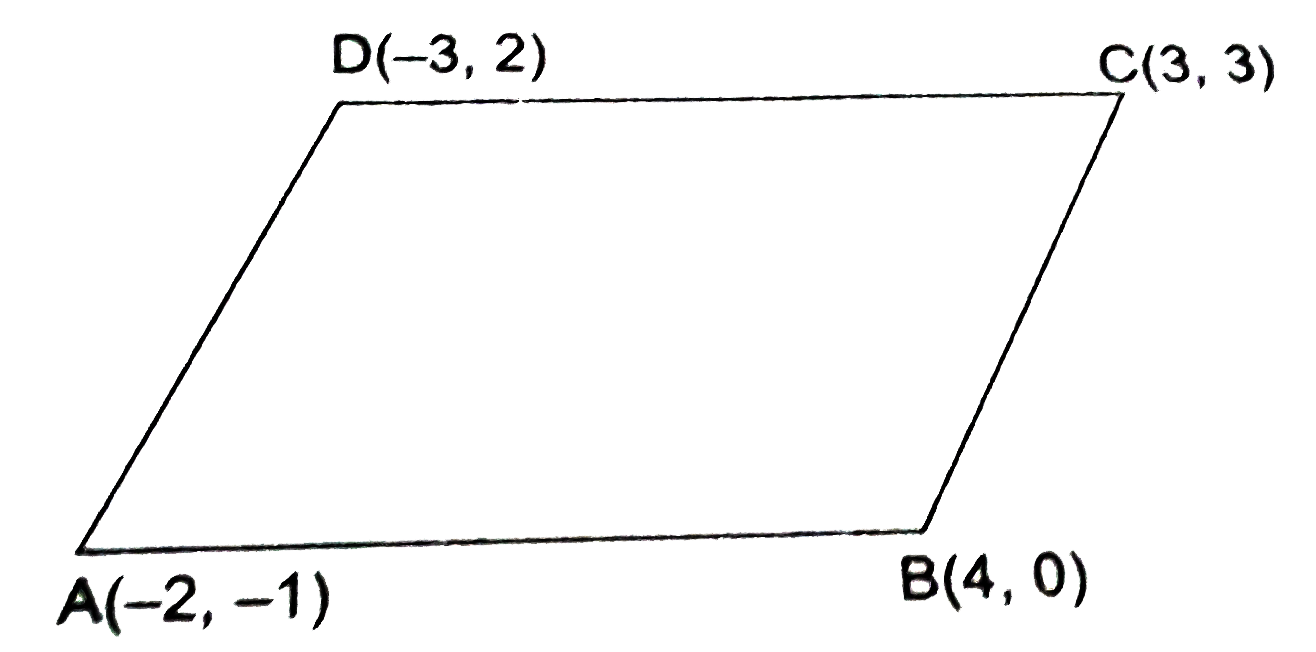
By using the concept of slope, show that the points (-2,-10, (4,0), (3,3) and (-3,2) are the vertices f a parallelogram.
Let A(-2,-1)B(4,0), C(3,3) and D(-3,2) be the vertices of the given quadrilateral ABCD. Then, slope of AB=0−(−1)4−(−2)=16
slope of DC=3−23−(−3)=16
slope of BC=3−03−4=3−1=−3
slope of AD=2−(−1)−3−(−2)=3−1=−3
∴ slope ofAB= slope of DC ⇒AB∣∣DC,
slope of BC= slope of AD ⇒BC∣∣AD.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - STRAIGHT LINES EXERCISE - SOLVED-EXAMPLE12videos
STRAIGHT LINES
- BOOK - RS AGGARWALCHAPTER - STRAIGHT LINES EXERCISE - MISCELLANEOUS PROBLEMS9videos
STRAIGHT LINES
- BOOK - RS AGGARWALCHAPTER - STRAIGHT LINES EXERCISE - EXERCISE 20K10videos
STRAIGHT LINES
- BOOK - RS AGGARWALCHAPTER - STATISTICSEXERCISE - EXERCISE 30D5videos
STATISTICS
- BOOK - RS AGGARWALCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - EXERCISE 26 C13videos
THREE-DIMENSIONAL GEOMETRY
Similar Questions
Prove that the points (−2,−1),(4,0),(3,3)and(−3,2) are the vertices of a parallelogram.
View SolutionBy using the concept of slope, show that (−2,−1),(4,0),(3,3)and(−3,2) are the vertices of a parallelogram.
View SolutionProve that the points (2,−1), (0,2), (3,3) and (5,0) are the vertices of a parallelogram .
View SolutionProve that the points (−2,−1),(1,0),(4,3)and(1,2) are the vertices of a parallelogram.
View SolutionShow that the point (3,−1,−1),(5,−4,0),(2,3,−2) and (0,6,−3) are the vertices of a parallelogram.
View SolutionUsing the slope of line, show that the points (−1,−2), (0,4), (3,3) and (2,−3) are the vertices of a parallelogram.
View SolutionShow that the points (3,-1,-1),(5,-4,0),(2,3,-2) and (0,6,-3) are the vertices of a parallelogram
View SolutionShow that the points A(1, −2), B(3, 6), C(5, 10) and D(3, 2) are the vertices of a parallelogram.
View SolutionProve that the points (3, −2), (4, 0), (6, −3) and (5, −5) are the vertices of a parallelogram.
View SolutionShow that the points (3,-1,-1),(5,-4,0) ,(2,3,-2) and (0,6,-3) are the vertices of a parallelogram
View Solution

