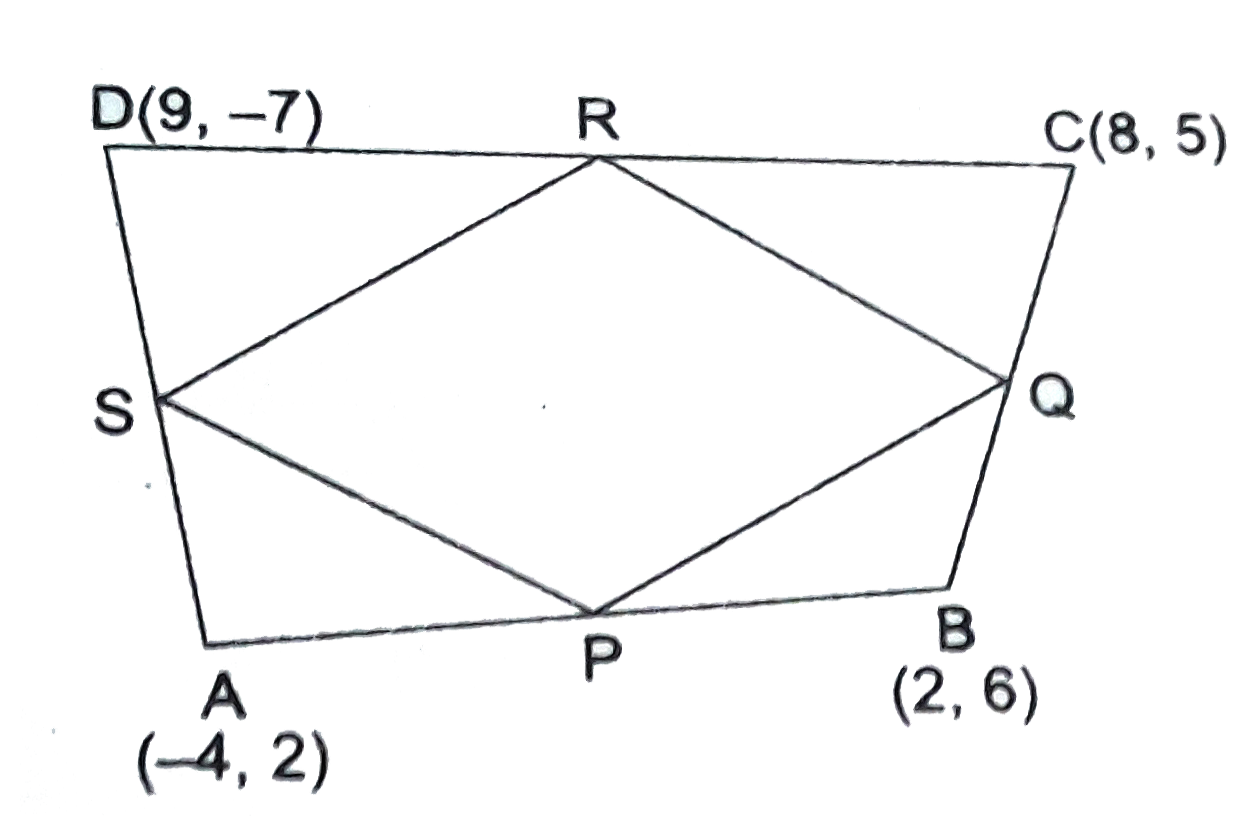
A quadrilateral has the vertices at the points $(- 4, 2), (2, 6), (8, 5) a n d (9, - 7)$ . Show that the mid points of the sides of this quadrilateral are the vertices of a parallelogram.

Video Solution

Text Solution

Verified by Experts

Clearly, the points P,Q,R,S are given by
$P (- 1, 4), Q (5, \frac{11}{2}), R (\frac{17}{2}, - 1) and S (\frac{5}{2}, \frac{- 5}{2})$
$∴ Slope of PQ = \frac{(\frac{11}{2} - 4)}{(5 + 1)} = \frac{3}{12} = \frac{1}{4}$
$Slope of SR = \frac{(- 1 + \frac{5}{2})}{(\frac{17}{2} - \frac{5}{2})} = \frac{3}{12} = \frac{1}{4}$
$Slope of QR = \frac{(- 1 + \frac{11}{2})}{(\frac{17}{2} - 5)} = (\frac{- 13}{2} \times \frac{2}{7}) = \frac{- 13}{7}$
$Slope of PS = \frac{(\frac{5}{2} - 4)}{(\frac{5}{2} + 1)} = (\frac{- 13}{2} \times \frac{2}{7}) = \frac{- 13}{7}$
$∴$ slope of PQ=slope of SR $\Rightarrow P Q ∣ ∣ S R$ ,
slope of QR=slope of PS $\Rightarrow Q R ∣ ∣ P S$ .
Hence, PQRS is a parallelgram.

Updated on:21/07/2023

A quadrilateral has the vertices at the points (-4, 2), (2, 6), (8, 5) and (9, -7). Show that the mid-points of the sides of this quadrilateral are the vertices of a parallelogram
ARectangle
BSquare
CParallelogram
DRhombus
Find the area of quadrilateral whose vertices are (-4,5) , (0,7), (5,-5) and (-4-2)
A $54 \frac{1}{2}$ sq. units
B $56 \frac{1}{2}$ sq. units
C $58 \frac{1}{2}$ sq. units
D $60 \frac{1}{2}$ sq. units
The figure formed by joining the mid-points of the sides of a quadrilateral taken in order is
Aparallelogram
Brectange
Csquare
Dnone