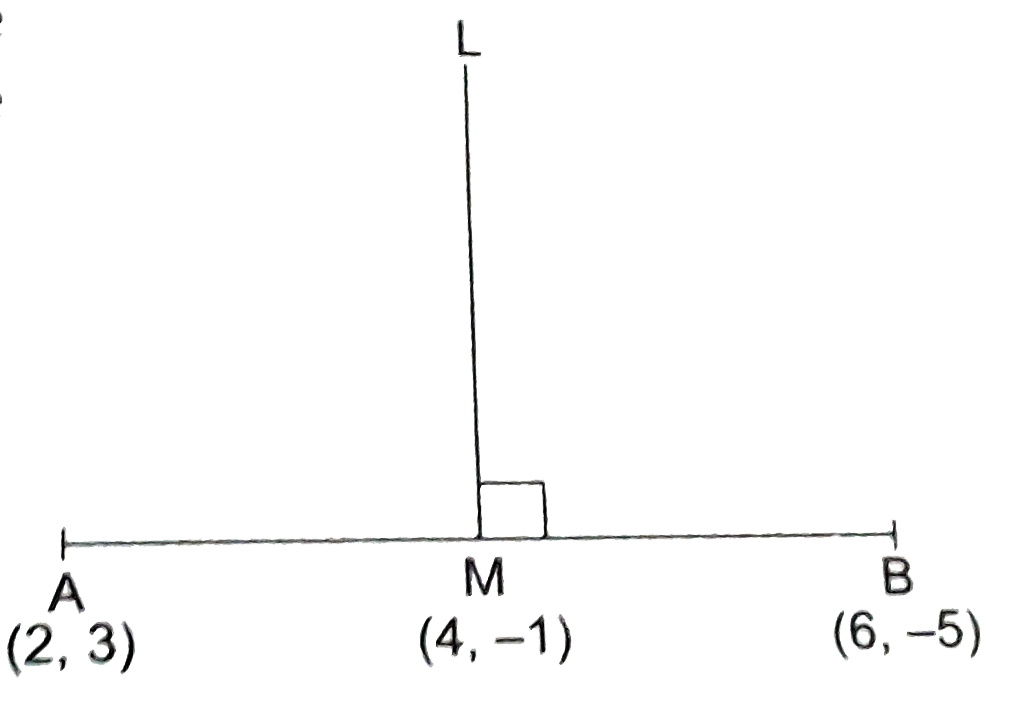
Find the equation of the perpendicular bisector of the line segment joining the points $A (2, 3)$ and $B (6, - 5)$

A

$x - 2 y - 6 = 0$

B

$3 x - 2 y - 6 = 0$

C

$x + 2 y + 6 = 0$

D

$x + 2 y - 6 = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Here, A(2,3) and B(6,-5) are the end points of the given line segment.
The midpoint of AB is $M (\frac{2 + 6}{2}, \frac{3 - 5}{2}) + N 65, i . e . M (4, - 1)$
Slope of AB= $\frac{- 5 - 3}{6 - 2} = - 2$
Let $L M perpendicular A B$ and let the slope of LM be m.
Then, $m \times (- 2) = - 1 \Rightarrow m = \frac{1}{2}$
Clearly, LM is the perpendicular bisector of AB.
Now, LM is a line with slope of $= \frac{1}{2}$ and passing through M(4,-1)
So, the required equation is
$\frac{y - (- 1)}{x - 4} = \frac{1}{2} \Rightarrow 2 (y + 1) = (x - 4)$
$\Rightarrow x - 2 y - 6 = 0$

Updated on:21/07/2023

|

Class 11 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

The equation of perpendicular bisector of the line segment joining the points (1, 2) and (–2, 0) is
A5x + 2y = 1
B4x + 6y = 1
C6x + 4y = 1
Dnone of these

RS AGGARWAL-STRAIGHT LINES -EXAMPLE

Home
Ask Doubt
Profile