A(2,3) , B(-2,1) and C(4,-3) are the vertices of $Δ A B C$ . Find the slope of (i) side AB (ii) altitude through A (iii) median through A (iv) perpendicular bisector of AB.

Video Solution

Text Solution

Verified by Experts

(i) Let F be the midpoint of side AB.
Then, CF is the median of through C.

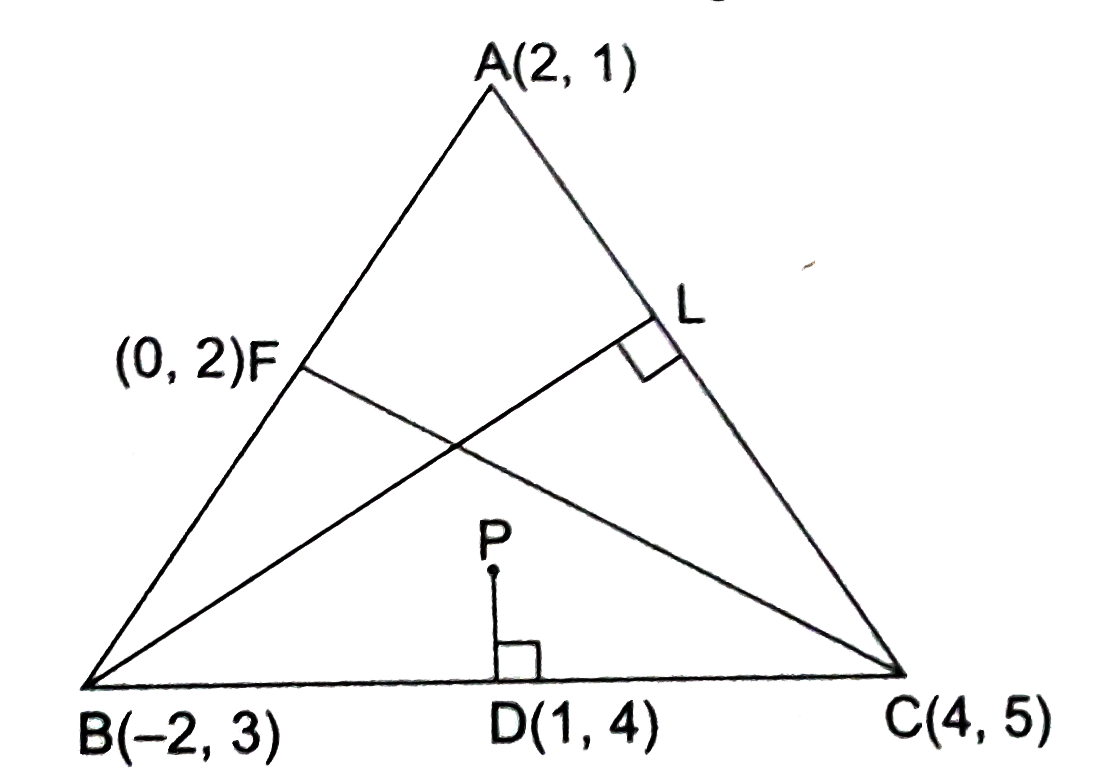
Coordinates of F are F $(\frac{2 + (- 2)}{2}, \frac{1 + 3}{2}), i . e . F (0, 2)$
So, the equation of median CF is given by
$\frac{y - 5}{x - 4} = \frac{2 - 5}{0 - 4} \Leftrightarrow \frac{y - 5}{x - 4} = \frac{3}{4}$
$\Leftrightarrow 4 (y - 5) = 3 (x - 4) \Leftrightarrow 3 x - 4 y + 8 = 0$
Hence, the equation of median CF is 3x-4y+8=0.
(ii) Draw $B L perpendicular A C$ . Then, BL is the altitude through B.
Slope of AC= $\frac{5 - 1}{4 - 2} = 2$
Let the slope of BL be m.
Since, $B L perpendicular A C$ , we have 2m=-1 and therefore, $m = \frac{- 1}{2}$
Thus, the slope of BL is $\frac{- 1}{2}$
So, the equation of BL is given by $\frac{y - 3}{x + 2} = \frac{- 1}{2} \Leftrightarrow 2 (y - 3) = - (x + 2) \Leftrightarrow x + 2 y - 4 = 0$
Hence, the equation of altitude BL is x+2y-4=0
Let D be the midpoint of BC.
Then, the coordinates of D are $D (\frac{- 2 + 4}{2}, \frac{3 + 5}{2}), i . e . D (1, 4)$
Through D, draw $D P perpendicular B C$ .
Slope of BC= $\frac{5 - 3}{4 + 2} = \frac{2}{6} = \frac{1}{3}$
Let the slope of PD be m.
Since $P D perpendicular B C$ , we have $m \times \frac{1}{3} = - 1 \Rightarrow m = - 3$
Slope, of PD is -3
So, hte equation of PD is given by
$\frac{y - 4}{x - 1} = 3 \Leftrightarrow - 3 (x + 1) = (y - 4) \Leftrightarrow 3 x + y - 7 = 0$ .
Hence, the equaton of the rightarrow bisecotr of BC is 3x+y-7=0.

Updated on:21/07/2023