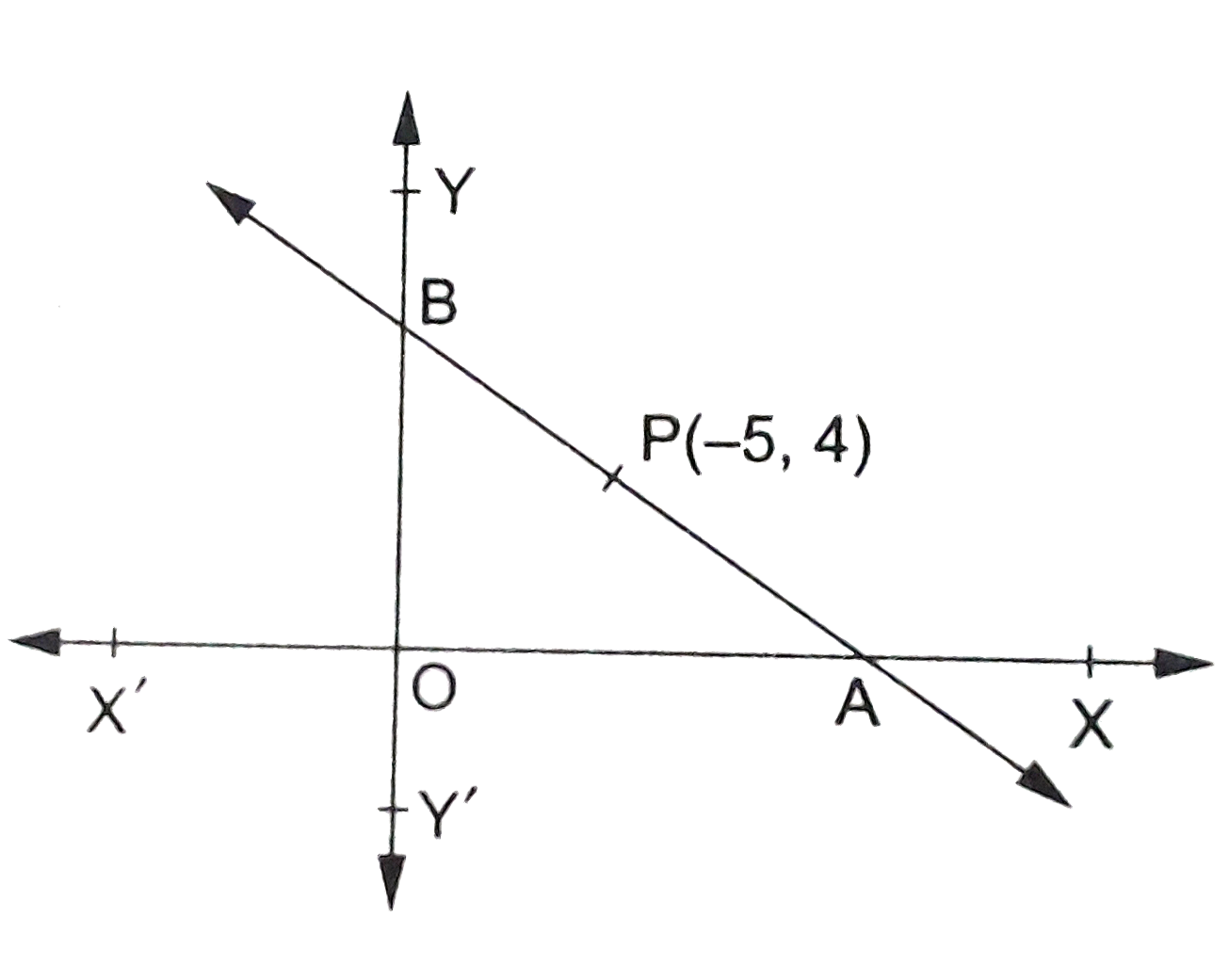
Find the equation of the line so that the segment intercept between the axes is divided by the point P(5,-4) in the ratio 1:2

Video Solution

Text Solution

Verified by Experts

Let AB be the given the line segment making intercept a and b on the x-axis and y-axis respectively. Then the equation of line AB is $\frac{x}{a} + \frac{y}{b} = 1$
So, these points are A(a,0) and B(0,b) Now, P(-5,4) divides AB in the ration 1:2
$∴ \frac{(1 \times 0 + 2 \times a)}{(1 + 2)} = - 5 and \frac{(1 \times b + 2 \times 0)}{(1 + 2)} = 4 \Leftrightarrow a = \frac{- 15}{2}, and b = 12$
So, hte required equation of the line is $\frac{x}{(\frac{- 15}{2})} + \frac{y}{12} = 1 \Leftrightarrow \frac{- 2 x}{15} + \frac{y}{12} = 1$
$\Leftrightarrow 8 x - 5 y + 60 = 0$
Hence, the required equation of the line is $8 x - 5 y + 60 = 0$ .

Updated on:21/07/2023

Find the equation of the line which cuts off intercepts 2 and 3 from the axes :
AEither x + y = 4 or 9x + y =12
BEither x + y = 5 or 4x + 9y = 30
CEither x + y = 4 or x + 9y = 12
DEither x + y = 5 or 9x + 4y = 30
The equation of the line, when the portion of it intercepted between the axes is divided by the point (2, 3) in the ratio of 3 : 2, is
AEither $x + y or 9 x + y = 12$
BEither $x + y = 5 or 4 x + 9 y = 30$
CEither $x + y = 4 or x + 9 y = 12$
DEither $x + y = 5 or 9 x + 4 y = 30$
If the portion of a line intercepted between the coordinate axes is divided by the point $(2, - 10$ in the ratio $3 : 2 .$ then the equation of that line is
A $5 x - 2 y - 20 = 0$
B $2 x - y - 5 = 0$
C $3 x - y - 7 = 0$
D $x - 3 y - 5 = 9$