Question

In a $\Delta ABC,\angle C={90}^{\circ }\text{and}\tan A=\frac{1}{\sqrt{3}}.$ find the values of :
$\left(i\right)(\sin A\cdot \cos B+\cos A\cdot \sin B)\left(ii\right)(\cos A\cdot \cos B-\sin A\cdot \sin B)$

Explanation

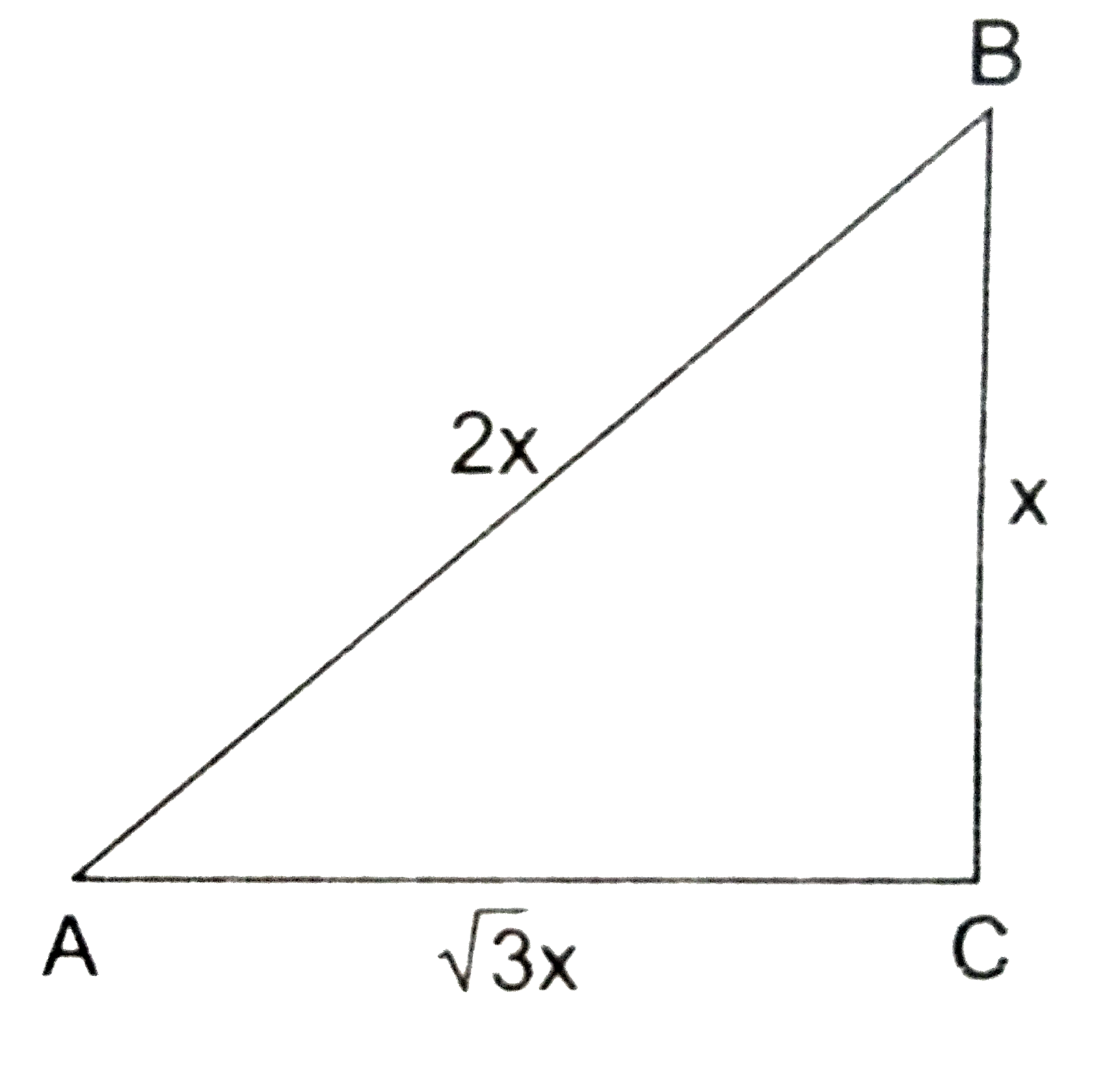
Consider a `Delta ABC "in which " angle C=90^(@) and tan A=(1)/(sqrt(3)).`
then , `tan A=(1)/(sqrt(3))implies(BC)/(AC)=(1)/(sqrt(3)).`
Let `BC=x ,"Then " ,AC=sqrt(3)x.`
BY pythagoras ' theorem , we have
`AB^(2)=AC^(2)BC^(2)`
`=(sqrt(3)x)^(2)+x^(2)=(3x^(2)+x^(2))=4x^(2)`
`implies AB=sqrt(4x^(2))=2x.`
For T- ratios of `angle A,` we have
base `=AC=sqrt(3)x,` perpendicular `=BC=x and `
hypotenuse `=AB=2x.`
`therefore sin A=(BC)/(AB)=(x)/(2x)=(1)/(2) and cos A=(AC)/(AB)=(sqrt(3)x)/(2x)=(sqrt(3))/(2).`
For T- ratios of `angle B,` we have
`"base" =BC=x, "perpendicular "=AC=sqrt(3)x and `
hypotenuse `=AB=2x.`
`therefore sin B=(AC)/(AB)=(sqrt(3)x)/(2x)=(sqrt(3))/(2)and cos B=(BC)/(AB)=(x)/(2x)=(1)/(2).`
`(i) (sin A* cos B + cos A*sin B)=((1)/(2)xx(1)/(2)+(sqrt(3))/(2)xx(sqrt(3))/(2))=((1)/(4)+(3)/(4))=1.`
`therefore (sin A* cos B + cos A* sin B)=1.`
`(ii) (cos A cos B-sin A sin B)=((sqrt(3))/(2)xx(1)/(2)-(1)/(2)xx(sqrt(3))/(2))=0.`
`therefore (cos A cos B- sin A sin B)=0.`