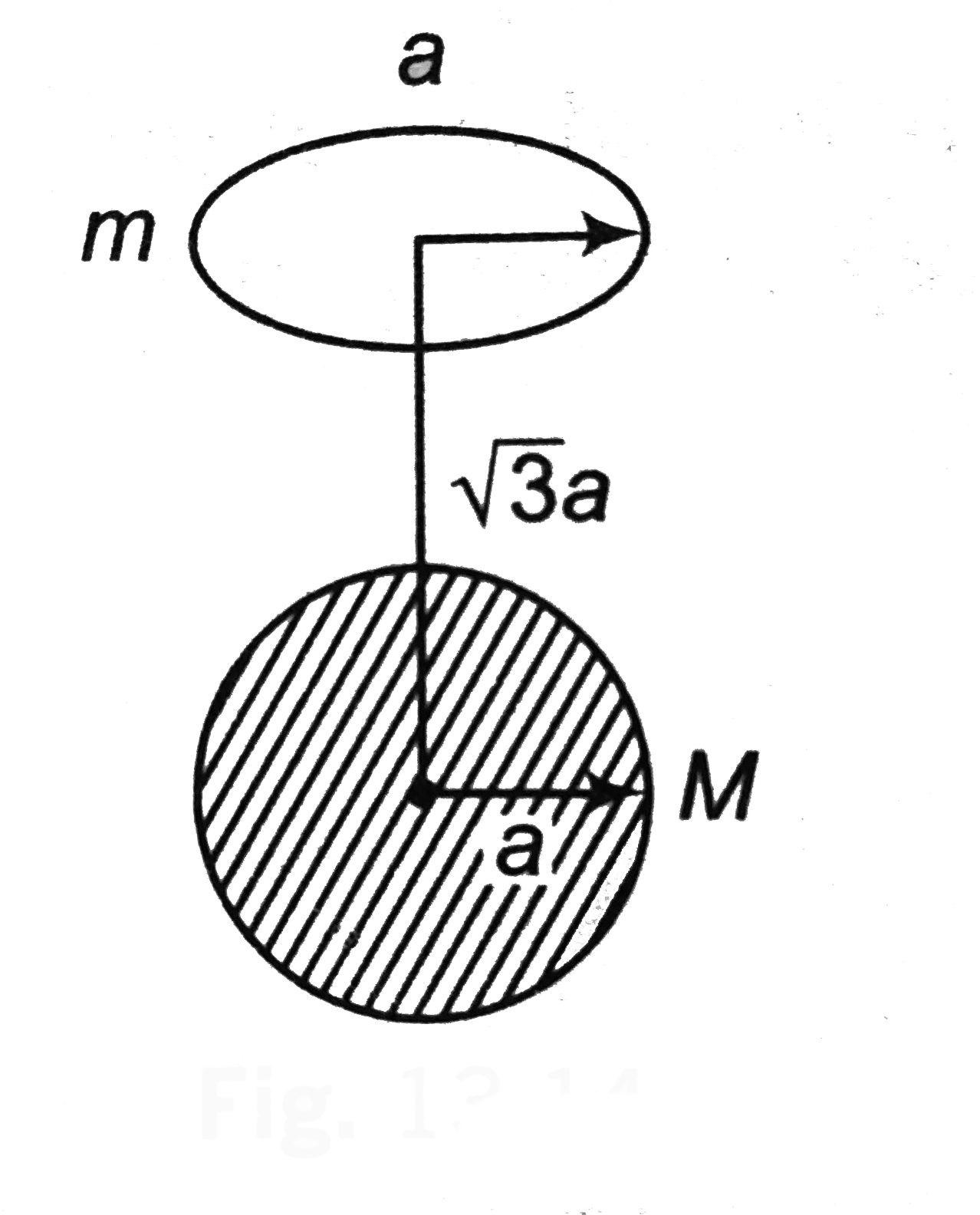
A uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
GMm8r2
GMm4r2
√3GMm8r2
GMm8r3√3
The correct Answer is:A, B, C
To find the gravitational force exerted by a uniform sphere on a uniform ring placed above it, we can follow these steps:
Step 1: Understand the Setup
We have a uniform ring of mass m and radius a positioned directly above a uniform sphere of mass M and radius a. The distance from the center of the sphere to the center of the ring is √3a.
Step 2: Calculate the Gravitational Field due to the Sphere at the Location of the Ring
The gravitational field Eg due to a spherical mass at a distance d from its center is given by:
Eg=GMd2
where G is the gravitational constant, M is the mass of the sphere, and d is the distance from the center of the sphere to the point where we are calculating the field.
In this case, the distance d is √3a:
Eg=GM(√3a)2=GM3a2
Step 3: Calculate the Gravitational Force on the Ring
The gravitational force F exerted by the sphere on the ring can be calculated using the formula:
F=m⋅Eg
Substituting the expression for Eg:
F=m⋅GM3a2
Step 4: Final Expression for the Gravitational Force
Thus, the gravitational force exerted by the sphere on the ring is:
F=GMm3a2
Summary
The gravitational force exerted by the sphere on the ring is given by:
F=GMm3a2
We have a uniform ring of mass m and radius a positioned directly above a uniform sphere of mass M and radius a. The distance from the center of the sphere to the center of the ring is √3a.
The gravitational field Eg due to a spherical mass at a distance d from its center is given by:
Eg=GMd2
where G is the gravitational constant, M is the mass of the sphere, and d is the distance from the center of the sphere to the point where we are calculating the field.
Eg=GM(√3a)2=GM3a2
The gravitational force F exerted by the sphere on the ring can be calculated using the formula:
F=m⋅Eg
Substituting the expression for Eg:
F=m⋅GM3a2
Thus, the gravitational force exerted by the sphere on the ring is:
F=GMm3a2
The gravitational force exerted by the sphere on the ring is given by:
F=GMm3a2
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.120videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.220videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 More Than One Correct10videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE10videos
KINEMATICS
Similar Questions
A uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The center of the ring is at a distance √3a from the center of the sphere. Find the gravitational force exerted by the sphere on the ring.
View SolutionFor a uniform ring of mass M and radius R at its centre
View SolutionThe figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is
 View Solution
View SolutionThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
View SolutionA uniform ring of mass m is lying at a distance √3 a from the centre of mass M just over the sphere (where a is the radius of the ring as well as that of the sphere). Find the magnitude of gravitational force between them .
 View Solution
View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solide sphere]
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solide sphere]
View SolutionA uniform metal sphere of radius R and mass m is surrounded by a thin uniform spherical shell of same mass and radius 4R. The centre of the shell C falls on the surface of the inner sphere. Find the gravitational fields at points A and B.
 View Solution
View SolutionA circular ring of mass M and radius 'a' is placed in a gravity free space. A small particle of mass m placed on the axis of the ring at a distance √3a from the center of the ring, is released from rest. The velocity with which the particle passes through the center of the ring is
View Solution

