When a particle of mass m moves on the x-axis in a potential of the fo

The focal length of a thin biconvex lens is $20 c m$ . When an object is moved from a distance of $25 c m$ in front of it to $50 c m$ , the magni-fication of its image changes from $m_{25} \to m_{50}$ . The ratio $\frac{m_{25}}{m_{50}}$ is.

01:37

View Solution

A vernier calipers has $1 m m$ marks on the main scale. It has $20$ equal divisions on the Vernier scale which match with $16$ main scale divisions. For this Vernier calipers, the least count is

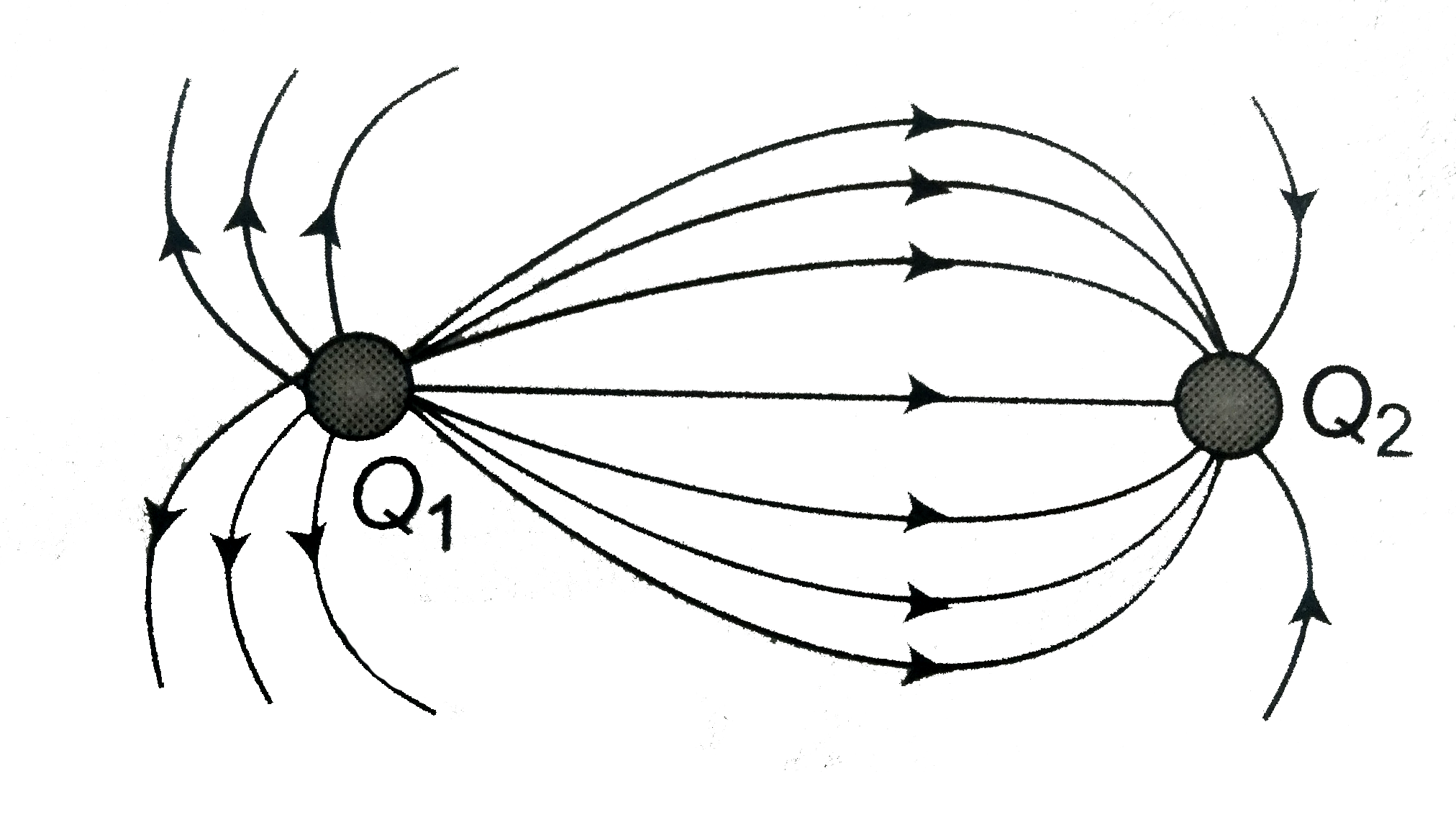
09:29

View Solution

A few electric field lines for a system of two charges $Q_{1}$ and $Q_{2}$ fixed at two different points on the $x$ -axis are shown in the figure. These lines suggest that
(i) $| Q_{1} | > | Q_{2} |$
(ii) $| Q_{1} | < | Q_{2} |$
(iii) At a finite distance to the left of $Q_{1}$ the electric field is zero
(iv) At a finite distance to the right of $Q_{2}$ the electric field is zero
ocr_image

06:19

View Solution

A spherical bubbles inside water has radius R . Take the pressuere in the bubbled and the water pressure to be pv. The bubble now gets compressed radially in an adiabatic manner so that its raduis becomes (R - a) . For $a < < R$ the magnitude of the work done in the process is given by $(4 π p o R a^{2})$ X. where X is a a constant and $y = C_{p} / C_{v} = 41 / 30$ . The value of X is

05:37

View Solution

Put a unifrom meter scale horizontally on your extended index fingers with the left one at 0.0 cm and the right one at 90.00 cm when you attempt to move both the fingers slowly towards the center , initially only the left finger slips with respect to to the scale and the right finger does not . after some distance, the left finger stops and the right one starts slipping . Then the right finger stops at a distance XR from the center (50.00 cm ) of the scale and the left one starts slopping again . This happens because to the difference in the fiictional forces on the two fingers . it the coefficients of static and dynamic between the fingers and the scale are 0.4 and 0.32 respectively , the value of XR (in cm is ...........

View Solution

A particle of mass 2 kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

06:11

View Solution

When a particle is mass m moves on the x- axis in a potential of the from V(x) = kx^(2) , it performs simple harmonic motion. The corresponding thime periond is proportional to sqrt((m)/(k)) , as can be seen easily asing dimensional analysis. However, the motion of a pariticle can be periodic even when its potential enem increases on both sides x = 0 in a way different from kx^(2) and its total energy is such that the particel does not escape to infinity. consider a particle of mass m moving onthe x- axis . Its potential energy is V(x) = alpha *x^4 (alpha gt 0 ) for |x| near the origin and becomes a constant equal to V_(0) for |x| ge X_(0) (see figure) If the total energy of the particle is E , it will perform is periodic motion why if :

02:54

View Solution

यदि किसी सरल आवर्त करते कण का मध्यमान स्थिति से विस्थापन x हो तो सरल आवर्त गति करते कण कि कुल ऊर्जा -

06:08

View Solution

आयाम a से सरल आवर्त गति करते हुए एक कण की गतिज एवं स्थितिज ऊर्जाएँ बराबर होंगी जब इसका विस्थापन है :

02:56

View Solution

जब m द्रव्यमान का एक कण :-अक्ष पर V(x) = $k x^{2}$ ', स्थितिज ऊर्जा से गतिमान होता है, तब यह सरल आवर्त गति करता है। इसका आवर्तकाल $\sqrt{\frac{m}{k}}$ के समानुपाती होता है, जो कि विमीय विश्लेषण द्वारा आसानी से निकाला जा सकता है। हालाँकि, यदि किसी एक कण की स्थितिज ऊर्जा x = 0 के दोनों तरफ $k x^{2}$ से । भिन्न तरह से बढ़े तथा कण की कुल ऊर्जा इतनी हो कि वह अनन्त तक पलायन न कर सके, तब भी कण की गति आवर्ती हो सकती है। m द्रव्यमान का एक कण x-अक्ष पर गति करता है जहाँ । x | के केन्द्र के पास होने पर स्थितिज ऊर्जा V(x) = $a x^{4}$ , (a>0) है तथा |x|> $X_{0}$ के लिए स्थितिज ऊर्जा V(x) = $V_{0}$ , है (चित्र देखें) .
Q. यदि एक कण की समग्र ऊर्जा E है, तो वह आवर्ती गति करेगा केवल जबकि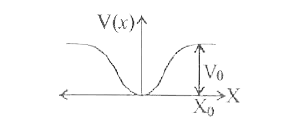
ocr_image

View Solution

जब m द्रव्यमान का एक कण :-अक्ष पर V(x) = $k x^{2}$ ', स्थितिज ऊर्जा से गतिमान होता है, तब यह सरल आवर्त गति करता है। इसका आवर्तकाल $\sqrt{\frac{m}{k}}$ के समानुपाती होता है, जो कि विमीय विश्लेषण द्वारा आसानी से निकाला जा सकता है। हालाँकि, यदि किसी एक कण की स्थितिज ऊर्जा x = 0 के दोनों तरफ $k x^{2}$ से । भिन्न तरह से बढ़े तथा कण की कुल ऊर्जा इतनी हो कि वह अनन्त तक पलायन न कर सके, तब भी कण की गति आवर्ती हो सकती है। m द्रव्यमान का एक कण x-अक्ष पर गति करता है जहाँ । x | के केन्द्र के पास होने पर स्थितिज ऊर्जा V(x) = $a x^{4}$ , (a>0) है तथा |x|> $X_{0}$ के लिए स्थितिज ऊर्जा V(x) = $V_{0}$ , है (चित्र देखें) .
Q. कम आयाम A के दोलन के लिए, कण का आवर्तकाल T निम्न में से किसके समानुपाती है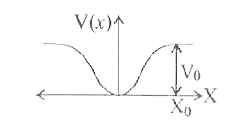
ocr_image

View Solution

जब m द्रव्यमान का एक कण :-अक्ष पर V(x) = $k x^{2}$ ', स्थितिज ऊर्जा से गतिमान होता है, तब यह सरल आवर्त गति करता है। इसका आवर्तकाल $\sqrt{\frac{m}{k}}$ के समानुपाती होता है, जो कि विमीय विश्लेषण द्वारा आसानी से निकाला जा सकता है। हालाँकि, यदि किसी एक कण की स्थितिज ऊर्जा x = 0 के दोनों तरफ $k x^{2}$ से । भिन्न तरह से बढ़े तथा कण की कुल ऊर्जा इतनी हो कि वह अनन्त तक पलायन न कर सके, तब भी कण की गति आवर्ती हो सकती है। m द्रव्यमान का एक कण x-अक्ष पर गति करता है जहाँ । x | के केन्द्र के पास होने पर स्थितिज ऊर्जा V(x) = $a x^{4}$ , (a>0) है तथा |x|> $X_{0}$ के लिए स्थितिज ऊर्जा V(x) = $V_{0}$ , है (चित्र देखें) .
Q |x|> $X_{0}$ के लिए कण का त्वरण-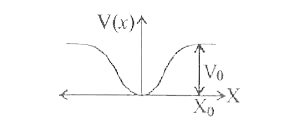
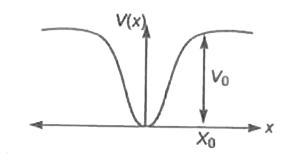
ocr_image