When a particle of mass m moves on the x-axis in a potential of the form it performs simple harmonic motion. The correspondubing time period is proprtional to , as can be seen easily using dimensional analusis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of in a way different from and its total energy is such that the particle does not escape toin finity. Consider a particle of mass m moving on the x-axis. Its potential energy is for |x| neat the origin and becomes a constant equal to for |x|impliesX_(0)|x|gtX_(0)V_(0)
(b) proportional to.
proportional to
Proportional to
proportional to
zero
The correct Answer is:D
Step by step video, text & image solution for When a particle of mass m moves on the x-axis in a potential of the form V(x) =kx^(2) it performs simple harmonic motion. The correspondubing time period is proprtional to sqrtm/h, as can be seen easily using dimensional analusis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x=0 in a way different from kx^(2) and its total energy is such that the particle does not escape toin finity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x)=ax^(4)(agt0) for |x| neat the origin and becomes a constant equal to V_(0) for |x|impliesX_(0) (see figure). (##JMA_CHMO_C10_033_Q01##). The acceleration of this partile for |x|gtX_(0) is (a) proprtional to V_(0) (b) proportional to. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - Section -IV (Integer type)10videos
JEE ADVANCED
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - Section-I (single correct choice type)6videos
JEE ADVANCED
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - Section-II (Multiple correct choice type)5videos
JEE ADVANCED
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE (ADVANCE) 2020EXERCISE - SECTION 36videos
JEE (ADVANCE) 2020
- BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCED 2020EXERCISE - SECTION-36videos
JEE ADVANCED 2020
Similar Questions
Knowledge Check
- Question 1 - Select One
When a particle of mass m moves on the X-axis in a potential of the form V(x)=kx2, it performs simple harmonic motion. The corresponding time period is proportional to
√mk, as can be seen easily using dimensional analysis.
However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the X-axis. Its potential energy is V(x) =ax2(a>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0
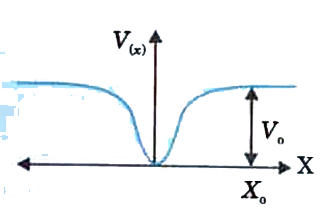
The acceleration of this particle for |X|>X0 isAproportional to (v0mX0)Bpropotinal to √V0mX0Cproportional to V0DZero - Question 2 - Select One
When a particle of mass m moves on the X-axis in a potential of the form V(x)=kx2, it performs simple harmonic motion. The corresponding time period is proportional to
√mk, as can be seen easily using dimensional analysis.
However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the X-axis. Its potential energy is V(x) =ax2(a>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0
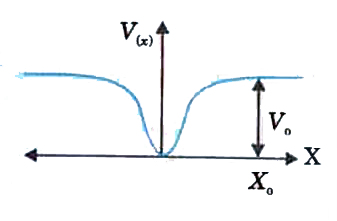
For periodic motion os small amplitude A . The time periodic T of this particle is proportional toAA√mαB1A√mαCA√αmD1A√αm - Question 3 - Select One
When a particle is mass m moves on the x− axis in a potential of the from V(x)=kx2, it performs simple harmonic motion. The corresponding thime periond is proportional to √mk, as can be seen easily asing dimensional analysis. However, the motion of a pariticle can be periodic even when its potential enem increases on both sides x=0 in a way different from kx2 and its total energy is such that the particel does not escape to infinity. consider a particle of mass m moving onthe x−axis . Its potential energy is V(x)=α⋅x4(α>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0 (see figure)
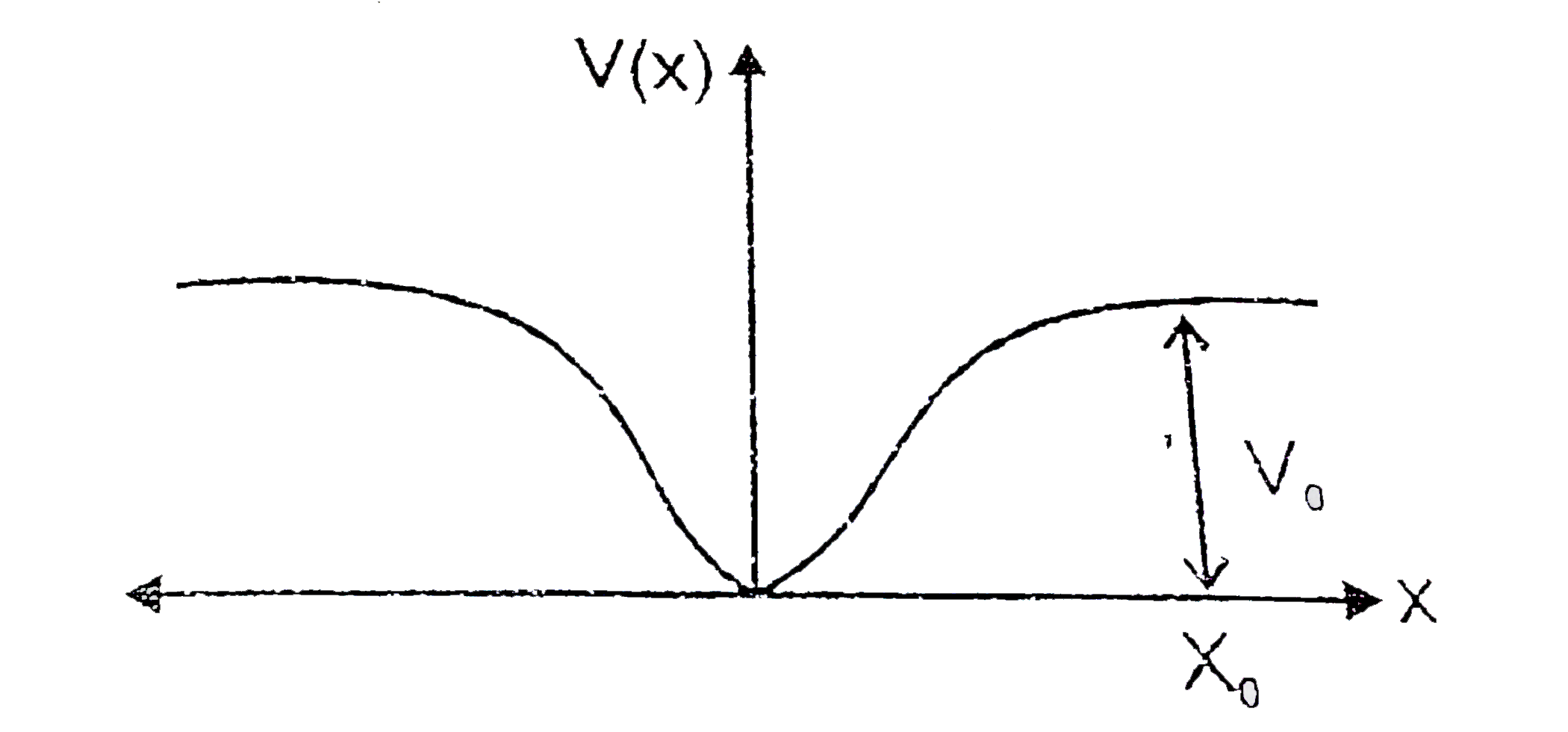
If the total energy of the particle is E, it will perform is periodic motion why if :AE<0BE>0CV0>E>0DE>V0
Apaticle of mass m moves in the potential energy U shown above. Find the period of the motion when the particle has total energy E.
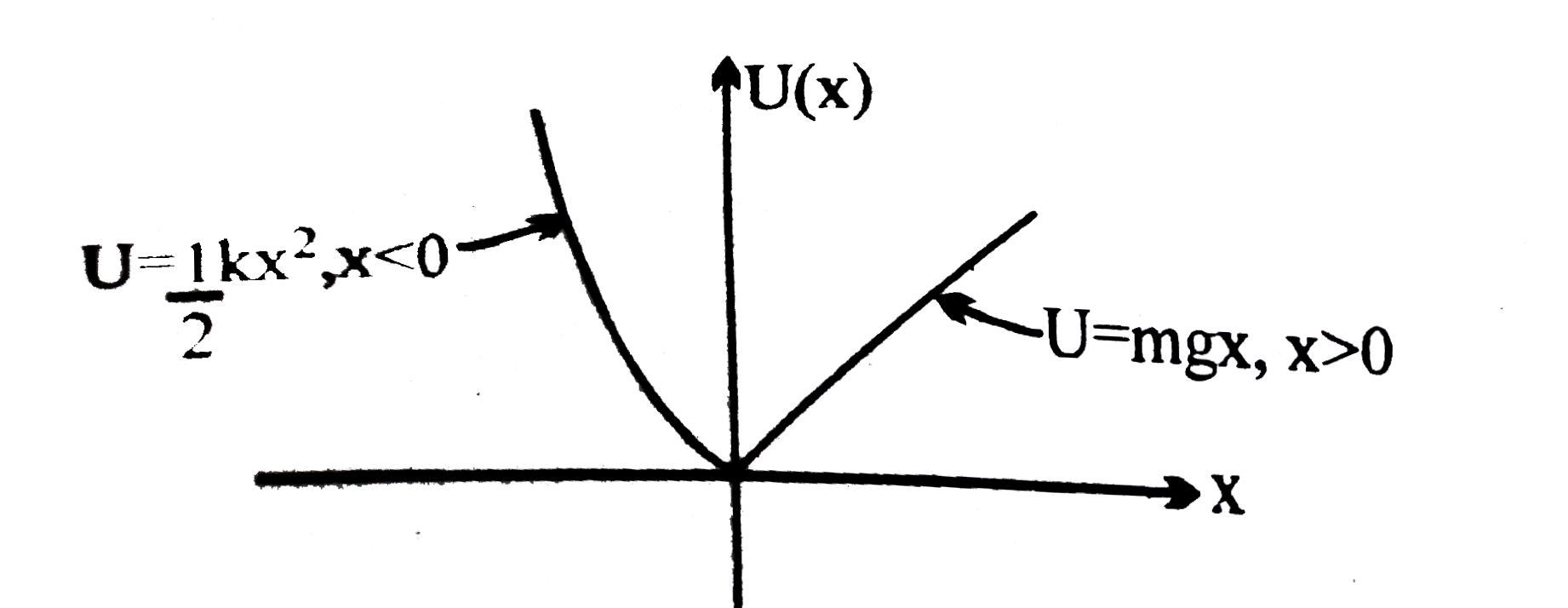 View Solution
View SolutionA particle moves on the X-axis according to the equation x=x0sin2ωt. The motion simple harmonic
View SolutionA particle is executing simple harmonic motion .Its total energy is proportional to its -
View SolutionIf particle is excuting simple harmonic motion with time period T, then the time period of its total mechanical energy is :-
View SolutionA particle of mass m moves in the potential energy U shoen above. The period of the motion when the particle has total energy E is
View Solution

