CD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. If ΔABC~ΔFEG, then show that
(i) CDGH=ACFG (ii) ΔDCB~ΔHGE (iii) ΔDCA~ΔHGFSolution in Bengali
Step by step video & image solution for CD and GH are respectively the bisectors of angle ACB and angle EGF such that D and H lie on sides AB and FE of Delta ABC and Delta FEG respectively. If Delta ABC ~ Delta FEG, then show that (i) (CD)/(GH) = (AC)/(FG) (ii) Delta DCB ~ Delta HGE (iii) Delta DCA ~ Delta HGF by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILAR TRIANGLES BOOK - NCERT BANGLISHCHAPTER - SIMILAR TRIANGLES EXERCISE - EXERCISE - 8.3
6 Videos
- SIMILAR TRIANGLES BOOK - NCERT BANGLISHCHAPTER - SIMILAR TRIANGLES EXERCISE - EXERCISE - 8.4
14 Videos
- SIMILAR TRIANGLES BOOK - NCERT BANGLISHCHAPTER - SIMILAR TRIANGLES EXERCISE - EXERCISE - 8.1
9 Videos
- SETSBOOK - NCERT BANGLISHCHAPTER - SETSEXERCISE - Try This
11 Videos
- STATISTICSBOOK - NCERT BANGLISHCHAPTER - STATISTICSEXERCISE - THINK AND DISCUSS
8 Videos
Similar Questions
D, E, F are mid points of sides BC, CA, AB of ΔABC. Find the ratio of areas of ΔDEFandΔABC.
View SolutionProve that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals
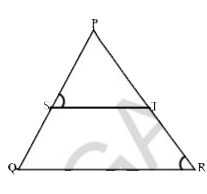
View SolutionIn ΔPQR, ST is a line such that PSSQ=PTTR and also ∠PST=∠PRQ.
Prove that ΔPQR is an isosceles triangle .
View SolutionWrite some sets of your choice, involving algebraic and geometrical ideas.
View SolutionThe mean value can be calculated from both ungrouped and grouped data. Which one do you think is more accurate? Why?
View SolutionIf in a triangle ABC,CD is the angular bisector of the angle ACB then CD is equal to
View SolutionCD और GH क्रमशः ∠ACBऔर ∠EFG के ऐसे समद्विभाजक है कि बिंदु Dऔर H क्रमशः ΔABCऔर ΔFEGकी भुजाओं ABऔर EFपर स्थित है। यदि ΔABC~ΔFEG है तो दर्शाइए कि :
(i)CDGH=AGFG
(ii)ΔDCB~ΔHGE
(iii)ΔDCA~ΔHGF
View SolutionIn the given figure, CD and GH are respectively the bisectors of angle ACB and angle FGE "of" Delta ABC and Delta EFG respectively . If Delta ABC~ Delta FEG , prove that : (a) Delta ADC~ Delta FHG " " (b) Delta BCD ~ Delta EGH " " ( c ) (CD)/(GH)=(AC)/(FG)
View SolutionΔABC में, ∠A का समद्विभाजक AD भुजा BC पर लम्ब है। दर्शाइए कि AB = AC है और ΔABC समद्विबाहु है।
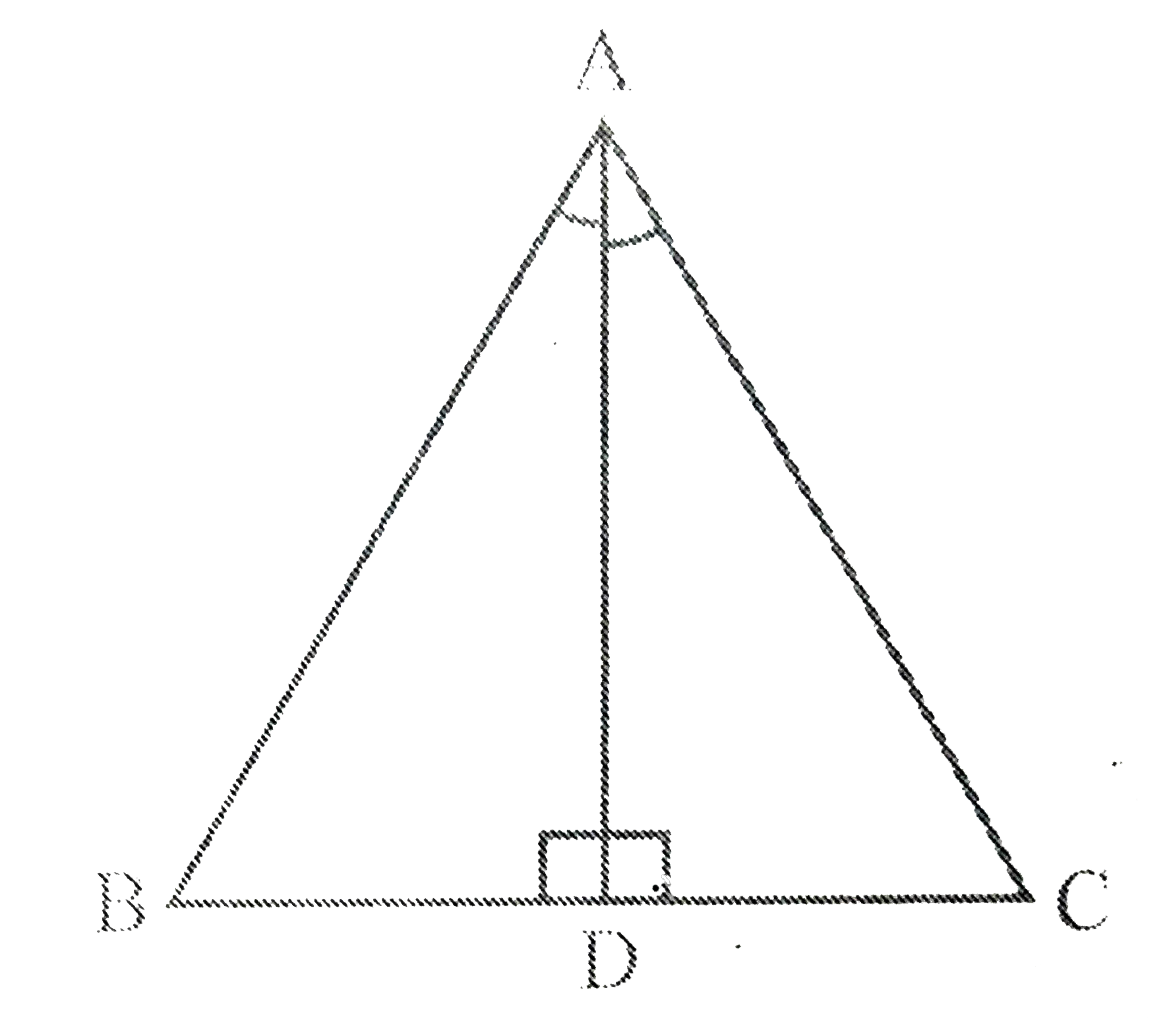
View SolutionΔABC में AD भुजा BC का लम्ब समद्विभाजक है। दर्शाइए कि ΔABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है।
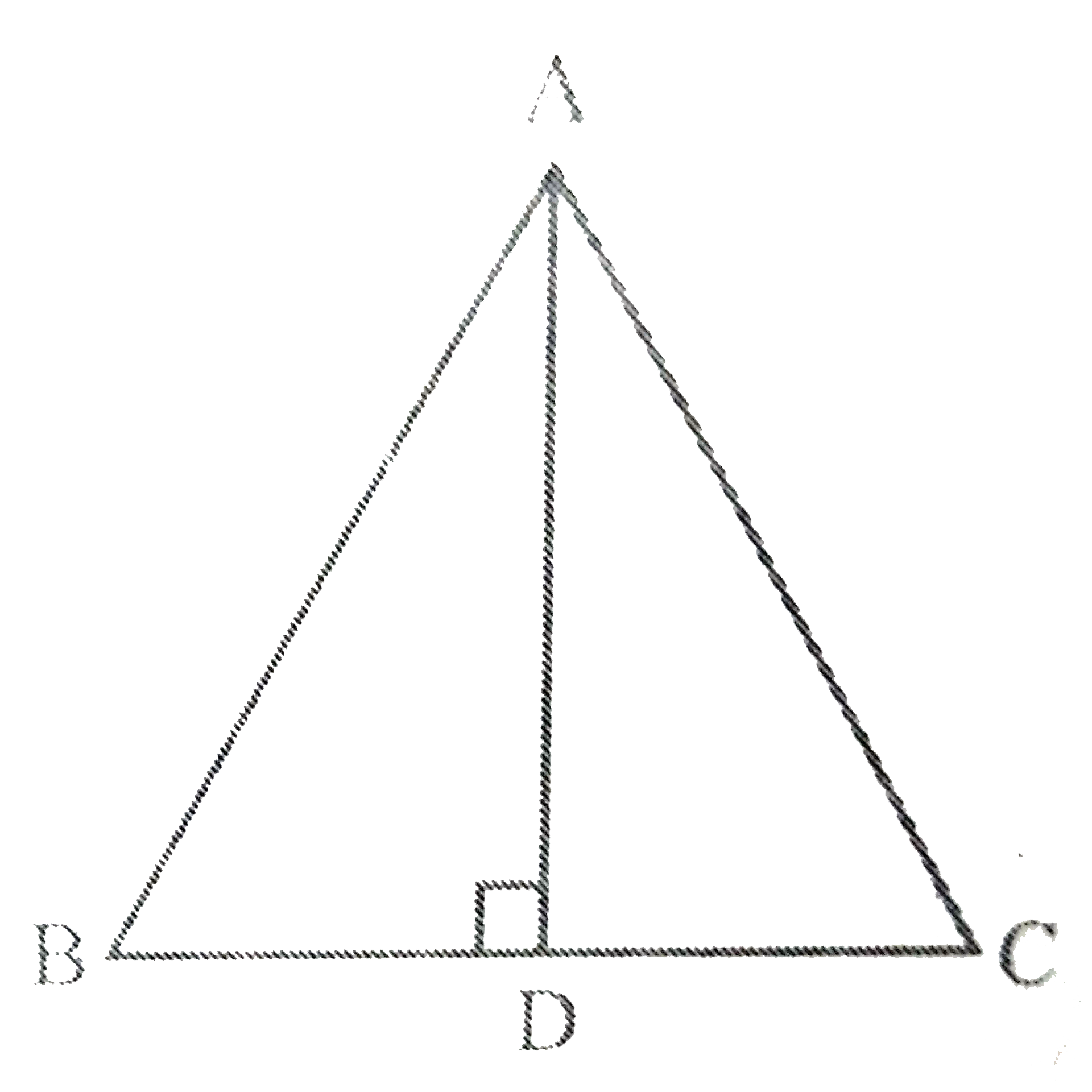
View Solution△ABC में ∠A का समद्विभाजक AD भुजा BC पर लम्ब है (आकृति देखिये) दर्शाइए की AB=AC है और △ABC समद्विभाजक है।
View Solutionत्रिभुजों ABC और EFG की भुजाओं AB और EF पर क्रमशः बिंदु D और H इस प्रकार है की CD और GH क्रमशः कोणों ∠ACB और ∠EGF के समद्विभाजक है|यदि ΔABC~ΔFEG हो, तो सिद्ध करो की:
ΔDCA~ΔHGF
View Solutionत्रिभुजों ABC और EFG की भुजाओं AB और EF पर क्रमशः बिंदु D और H इस प्रकार है की CD और GH क्रमशः कोणों ∠ACB और ∠EGF के समद्विभाजक है|यदि ΔABC~ΔFEG हो, तो सिद्ध करो की:
ΔDCB~ΔHGE
View Solutionचित्र में ,CD और GH क्रमशः ΔABC और ΔEFG की मध्यिकाएँ है|यदि ΔABC~ΔEFG हो,तो सिद्ध करों की :
ΔADC~ΔFHG
View SolutionCD और GH क्रमशः ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिन्दु D और H क्रमशः ΔABC और ΔEFG की भुजाओं AB और FE पर स्थित हैं । यदि ΔABC~ΔFEG तो दर्शाइए कि
(i) CDGH=ACFG
(ii) ΔDCB~ΔHGE
(iii) ΔDCA~ΔHGF
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
CDGH=ACFG
View Solution
