Obtain the maximum kinetic energy of b-particles, and the radiation frequencies of g decays in the decay scheme shown in Fig. You are given that
m(198Au)=197.968233u
m(198Hg)=197.966760u.

Kmax(β−1)=0.284MeV,Kmax(β−2)=0.960MeV
v(γ1)=2.627×1020Hz,v(γ2)=0.995×1020Hz,v(γ3)=1.632×1020Hz
Topper's Solved these Questions
- NUCLEIBOOK - NCERT BANGLISHCHAPTER - NUCLEIEXERCISE - EXERCISE
22 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT BANGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - ADDITIONAL EXERCISES
16 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT BANGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - EXERCISES
38 Videos
Similar Questions
Obtain the maximum kinetic energy of β-particles, and the radiation frequencies of γ decays in the decay scheme shown in Fig. 14.6. You are given that m(.198Au)=197.968233u,m(.198Hg)=197.966760u
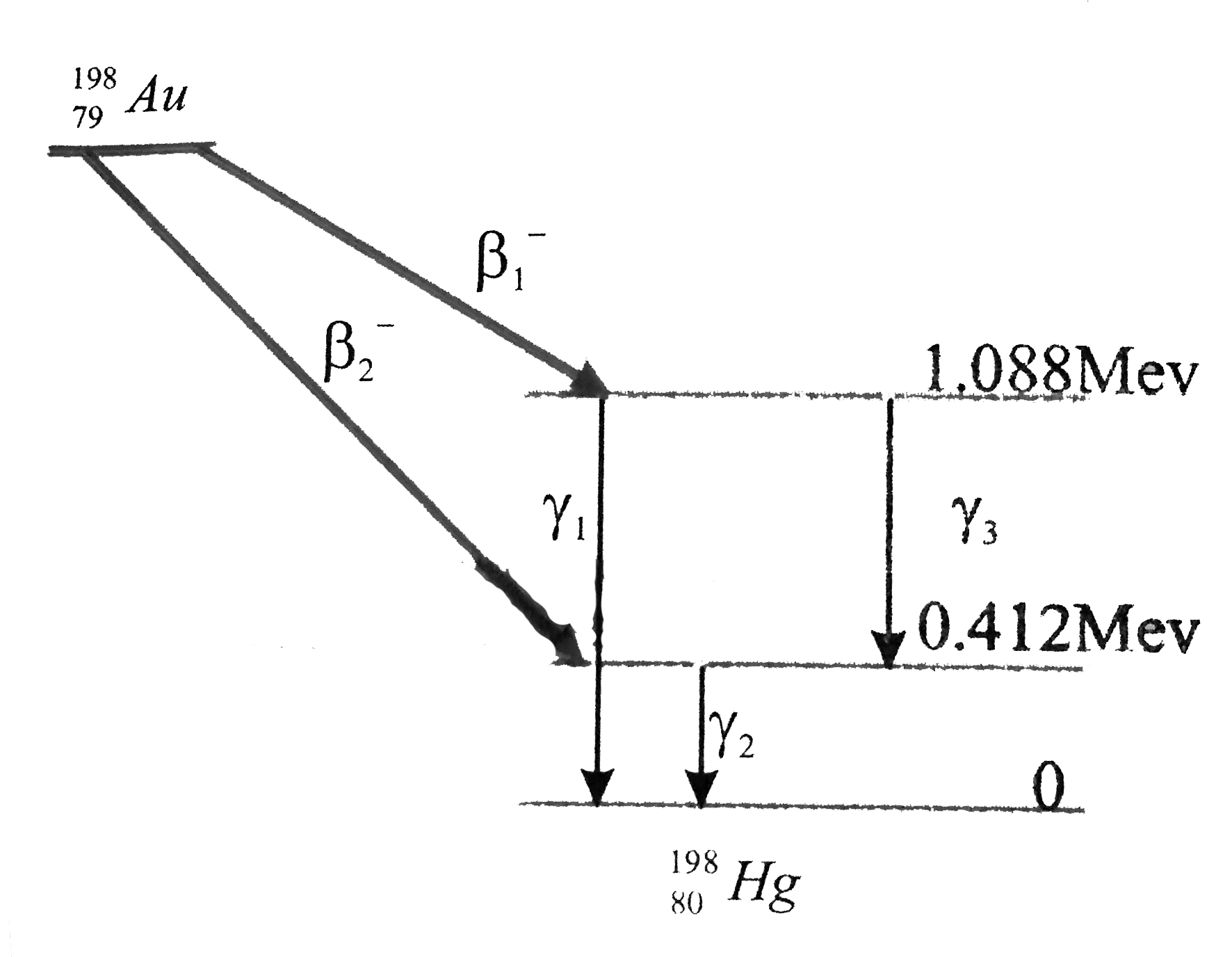
View SolutionObtain the maximum kinetic energy of β-particles, and the radiation frequencies of γ decays in the decay scheme shown in Fig. 14.6. You are given that m(.198Au)=197.968233u,m(.198Hg)=197.966760u

View SolutionCalculate the kinetic energy of β-particles and the radiation frequencies corresponding to the γ-decays shown in figure.
Given, mass of .12Mg27 atom =26.991425 amu and mass of .13Al27 atom = 26.990080 amu

View SolutionCalculate the kinetic energy of β-particles and the radiation frequencies corresponding to the γ-decays shown in figure.
Given, mass of .12Mg27 atom =26.991425 amu and mass of .13Al27 atom = 26.990080 amu

View SolutionA nucleus 10Ne23 undergoes β- decay and becomes 11Na23 . Calculate the maximum kinetic energy of electrons emitted assuming that the daughter nucleus and antineutrino carry negligible kinetic energy. Given mass of 10Ne23 = 22.994466 u and mass of 11Na23 = 22.989770 m
View SolutionFind the Q-value and the kinetic energy of the emitted o-particle in the a-decay of
(a) 22688Ra and (b) 22086Rn.
Given : m( 226Ra88)=226.02540 u, m( 22286Rn)=222.01750 u, m( 22086Rn)=220.01137u, m( 21684Po)=216.00189 u.
View SolutionFind the maximum energy that β- particle may have in the following decay:
8O19→9F19+−1e0+→v
Given m(8O19)=19.003576a.m.u.
m(9F19)=18.998403a.m.u.
m(−e0)=0.000549a.m.u.
View SolutionCalculate the maximum energy that a β particle can have in the following decay:
.8O19→.9F19+.−1e0+¯¯¯V
Given, m(.8O19)=19.003576u,m(.9F19)=18.998403u,m(.−1e0)=0.000549u
View SolutionConsider one of the fission reactions of U235 by thernmal neutrons :
.92U235+n→.38Sr94+.54Ce140+2n
The fission fragments are, however, not stable. They unaergo successive β−decays unit .38Sr94 becomes .40Zr94 and .54Xe140 becomes .58Ce140. Estimate the total energy released in the process. Is all that energy available as kinetic energy of the fission products (Zr and Ce)? You are given that
m(U235)=255.0439amu, mn=1.00866amu m(Zr94)=93.9065amu, m(Ce140)=139.9055amu
View SolutionCalculate the maximum energy that a β particle can have in the following decay:
.8O19→.9F19+.−1e0+¯ν
Given, m(.8O19)=19.003576u,m(.9F19)=18.998403u,m(.−1e0)=0.000549u
View Solution
