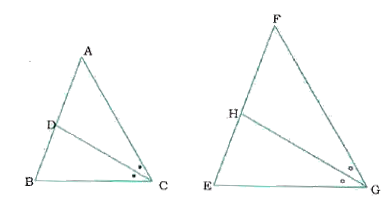
GD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
CDGH=ACFG Solution in Kannada
Step by step video & image solution for GD and GH are respectively the bisectors of angleACB and angleEGF such that D and H lie on sides AB and FE of DeltaABC and and DeltaEFG respectively. If DeltaABC~DeltaFEG , show that: (CD)/(GH) =(AC)/(FG) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILAR TRIANGLES BOOK - NCERT KANNADCHAPTER - SIMILAR TRIANGLES EXERCISE - EXERCISE - 8.3
6 Videos
- SIMILAR TRIANGLES BOOK - NCERT KANNADCHAPTER - SIMILAR TRIANGLES EXERCISE - EXERCISE - 8.4
9 Videos
- SIMILAR TRIANGLES BOOK - NCERT KANNADCHAPTER - SIMILAR TRIANGLES EXERCISE - EXERCISE - 8.1
4 Videos
- SETSBOOK - NCERT KANNADCHAPTER - SETSEXERCISE - Try This
11 Videos
- TANGENTS AND SECANTS TO A CIRCLEBOOK - NCERT KANNADCHAPTER - TANGENTS AND SECANTS TO A CIRCLEEXERCISE - Try this
3 Videos
Similar Questions
D, E, F are mid points of sides BC, CA, AB of ΔABC. Find the ratio of areas of ΔDEFandΔABC.
View SolutionProve that sum of the squares of the side of a rhombus is equal to the to the sum of the squares of its diagonals.
View SolutionUsing Theorem , prove that a line drawn thought the mid- point of one side of a triangle parallel to another side bisects the third side .( Recall that you have proved it in class IX).
View SolutionWrite some sets of your choice, involving algebraic and geometrical ideas.
View SolutionHow can you prove the converse of the above theorem.
" If a line in the plane of a circle is perpendicular to the radius at its endpoint on the circle, then the line is tangent of the circle ".
View SolutionCD और GH क्रमशः ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिन्दु D और H क्रमशः ΔABC और ΔEFG की भुजाओं AB और FE पर स्थित हैं । यदि ΔABC~ΔFEG तो दर्शाइए कि
(i) CDGH=ACFG
(ii) ΔDCB~ΔHGE
(iii) ΔDCA~ΔHGF
View SolutionCD and GH are the bisectors of ∠ACB and ∠EGF respectively. If D lies on AB of ΔABC and H lies on EF of ΔEFG and if ΔABC~ΔEFG, then prove that (a) CDGH=ACFG, (b)ΔDCB~ΔHGE, (c)ΔDCA~ΔHGF
View SolutionCD और GH क्रमशः ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिन्दु D और H क्रमशः ΔABC और ΔEFG की भुजाओं AB और FE पर स्थित हैं । यदि ΔABC~ΔFEG तो दर्शाइए कि
(i) CDGH=ACFG
(ii) ΔDCB~ΔHGE
(iii) ΔDCA~ΔHGF
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
CDGH=ACFG
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
ΔDCB~ΔHGE
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
ΔDCA~ΔHGF
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
CDGH=ACFG
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
ΔDCB~ΔHGE
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
ΔDCA~De<HGF
View SolutionCD and GH are respectively the bisectors of ⌊ACBand⌊EGF such that D and H lie on sidea AB and FE of ΔABCandΔEFG respectively. If ΔABC~ΔFEG, show that.
i] CDGH=ACFG
ii] ΔCDB~ΔHGE
iii] ΔDCA~ΔHGF
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG, show that :
CDGH=ACFG
View Solution
