PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR . Show that PM2=QM.MR . Solution in Kannada
Step by step video & image solution for PQR is a triangle right angled at P and M is a point on QR such that PM bot QR . Show that PM^(2) = QM . MR . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILAR TRIANGLES BOOK - NCERT KANNADCHAPTER - SIMILAR TRIANGLES EXERCISE - OPTIONAL EXERCISE
2 Videos
- SIMILAR TRIANGLES BOOK - NCERT KANNADCHAPTER - SIMILAR TRIANGLES EXERCISE - TRY THIS
3 Videos
- SIMILAR TRIANGLES BOOK - NCERT KANNADCHAPTER - SIMILAR TRIANGLES EXERCISE - EXERCISE - 8.3
6 Videos
- SETSBOOK - NCERT KANNADCHAPTER - SETSEXERCISE - Try This
11 Videos
- TANGENTS AND SECANTS TO A CIRCLEBOOK - NCERT KANNADCHAPTER - TANGENTS AND SECANTS TO A CIRCLEEXERCISE - Try this
3 Videos
Similar Questions
The diagonal AC of a parallelogram ABCD intersects DP at the point Q, where ‘P’ is any point on side AB. Prove that CQ×PQ=QA×QD.
View SolutionE and F are points on the sides PQ and PR respectively of Δ PQR. For each of the following cases, state whether EF || QR:
(i) PE=3.9cm,EQ=3cm,PF=3.6cm,FR=2.4cm
(ii) PE=4cm,QE=4.5cm,PF=8cm,RF=9cm
(iii) PQ=1.28cm,PR=2.56cm,PE=0.18cm,PF=0.36cm
View SolutionD, E, F are mid points of sides BC, CA, AB of ΔABC. Find the ratio of areas of ΔDEFandΔABC.
View SolutionWrite some sets of your choice, involving algebraic and geometrical ideas.
View SolutionHow can you prove the converse of the above theorem.
" If a line in the plane of a circle is perpendicular to the radius at its endpoint on the circle, then the line is tangent of the circle ".
View SolutionPQR is a triangle right-angled at P and M is a point on QR such that PM⊥QR. Show thatPM2=QM.MR.
View SolutionIn ΔPQR, D is the mid-point of ¯¯¯¯¯¯QR.then¯¯¯¯¯¯¯PM is ___________,PD is___________. Is QM=MR?
View SolutionIn PQR, QM⊥PR and PR2−PQ2=QR2 . Prove that QM2=PM×MR
View SolutionIn ∠PQR,PQ=6cm,PR=9cm and M is a point on QR such that it divides QR in the ratio 1:2PM⊥QR. Find QR.
View SolutionPQR एक समकोण त्रिभुज है जिसका कोण P समकोण है तथा QR पर बिंदु M इस प्रकार स्थित है कि PM⊥QR है । दर्शाइए कि PM2=QM.MR है ।
View Solutionयदि ΔPQR में, QM⊥PR तथा PR2−PQ2=QR2 हो तो सिद्ध करो की QM2=PM×MR
View SolutionPQR एक समकोण त्रिभुज है जिसका कोण P समकोण है तथा QR पर बिंदु M इस प्रकार स्थित है कि PM⊥QR है दर्शाइए कि PM2=QM.MR है
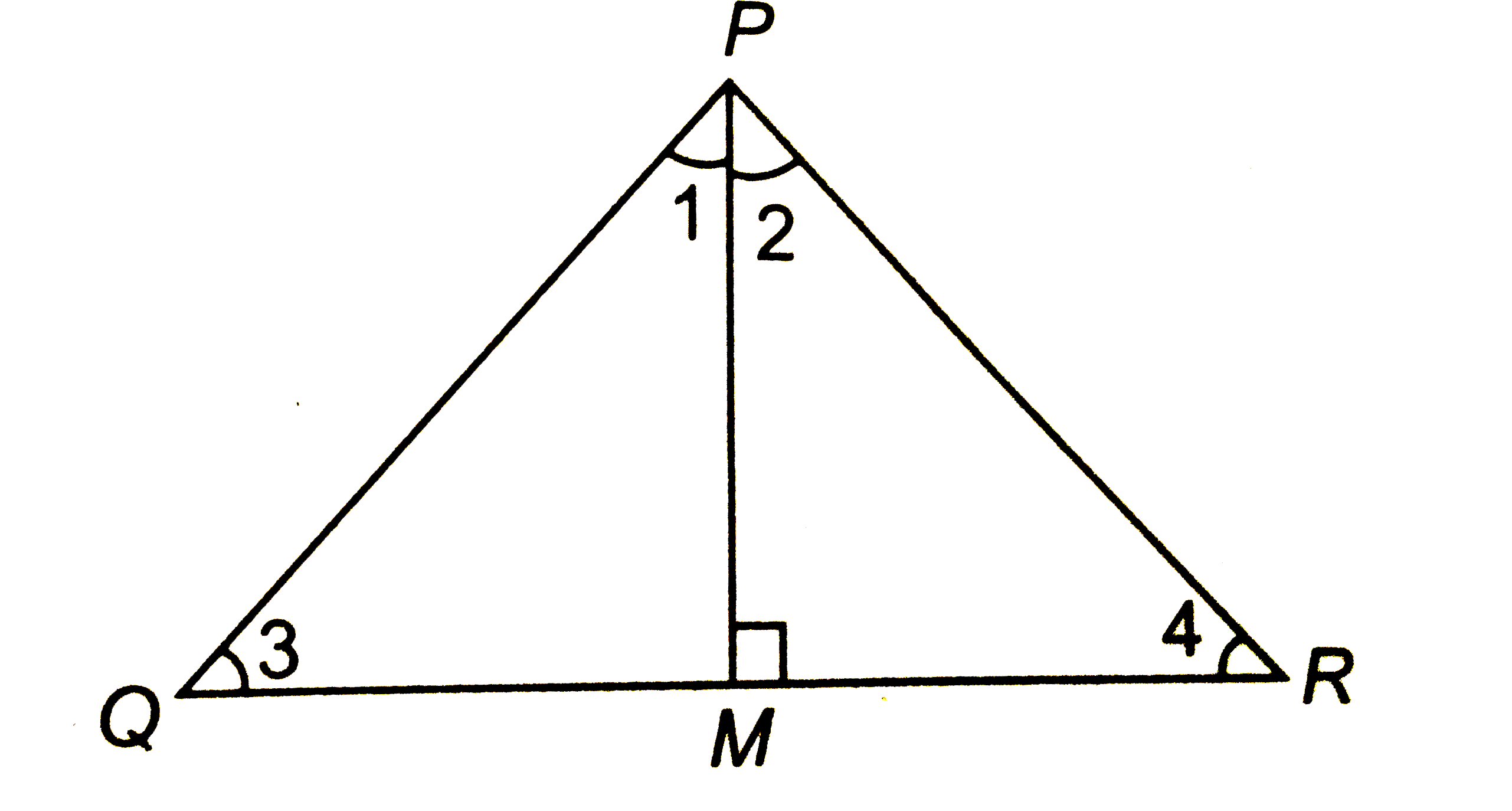
View SolutionPQR is a Triangle right angled at P and M is a point on QR such that PM⊥QR. Show that PM2=QM.MR.
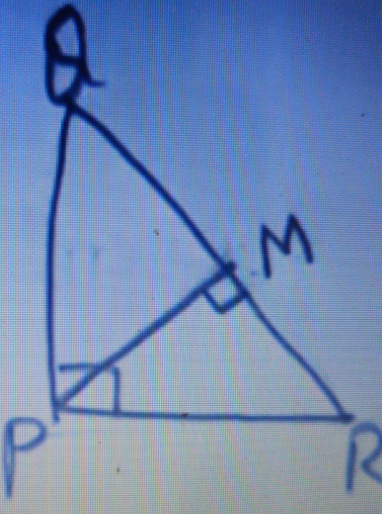
View SolutionPQR is a triangle right angled at P and M is a point on QR such that PM⊥QR . Show that PM2=QM.MR.
View SolutionPQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR . Show that PM2=QM.MR .
View SolutionPQR త్రిభుజంలో లంబకోణము శీర్షము 'P' వద్ద కలదు. PM⊥QR అగునట్లు QR పై బిందువు M అయిన PM2=QM.MR అని చూపండి.
View Solution
