The area of the triangle formed by joining the origin to the point of intersection of the line $x \sqrt{5} + 2 y = 3 \sqrt{5}$ and the circle $x^{2} + y^{\circ} = 10$ is 3 (b) 4 (c) 5 (d) 6

A

3

B

4

C

5

D

6

Video Solution

Text Solution

Verified by Experts

The correct Answer is:3

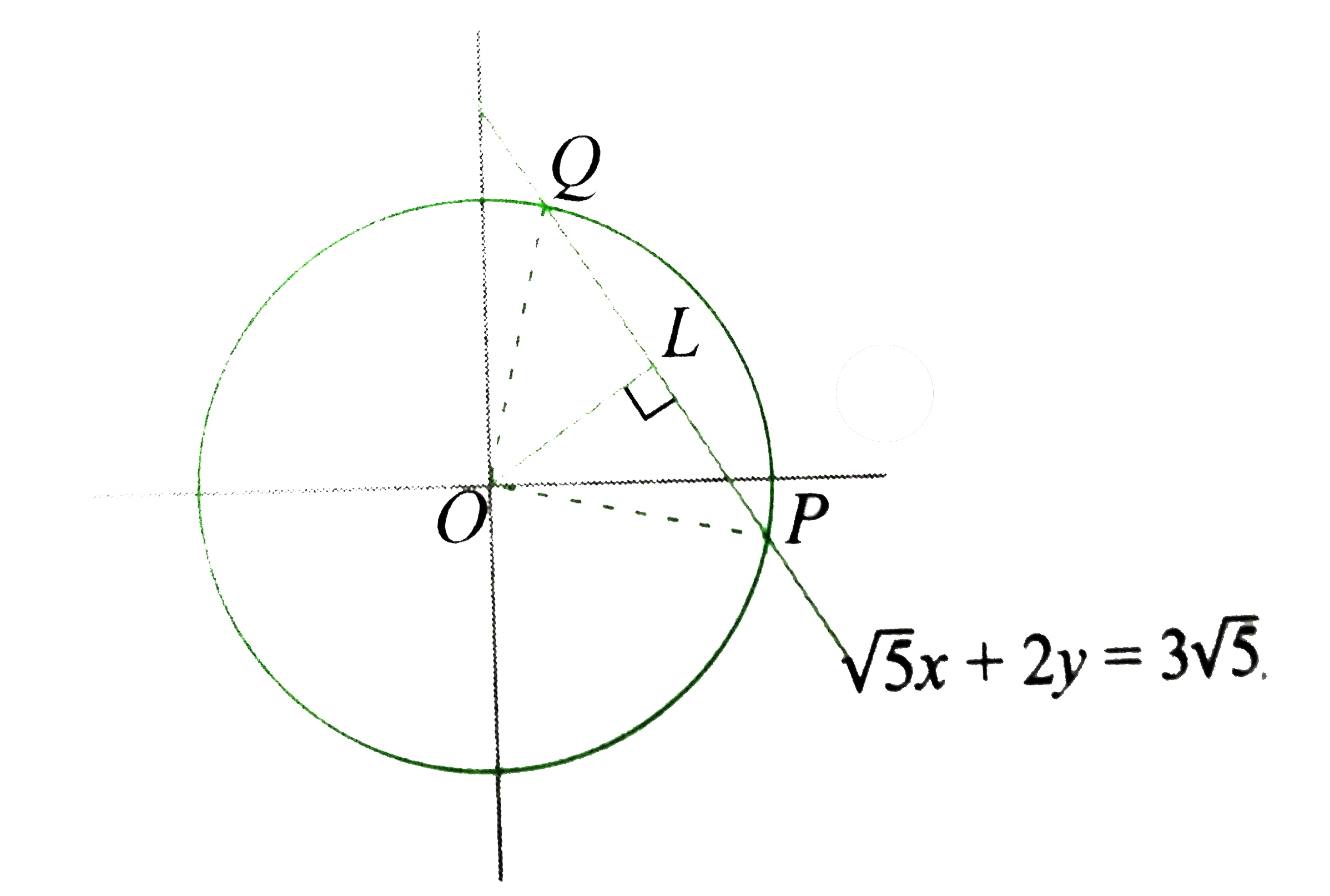
The length of perpendicular from the origin to the line $x \sqrt{5} + 2 y = 3 \sqrt{5}$ is
$O L = \frac{3 \sqrt{5}}{\sqrt{{(\sqrt{5})}^{2}} + 2^{2}} = \frac{3 \sqrt{5}}{\sqrt{9}} = \sqrt{5}$
Radius of the given circle $\sqrt{10} = O Q = O P$
$P Q = 2 Q L = 2 \sqrt{O Q^{2} - O L^{2}}$
$2 \sqrt{10 - 5} = 2 \sqrt{5}$
Thus, area of $Δ O P Q = \frac{1}{2} \times P Q \times O L$
$\frac{1}{2} \times 2 \sqrt{5} \times \sqrt{5} = 5$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The area of the triangle formed by joining the origin to the point of intersection of the line $x \sqrt{5} + 2 y = 3 \sqrt{5}$ and the circle $x^{2} + y^{\circ} = 10$ is 3 (b) 4 (c) 5 (d) 6
A3
B4
C5
D6
Question 2 - Select One
The acute angle between the lines joining the origin to the points of intersection of the line $\sqrt{3} x + y = 2$ and the circle $x^{2} + y^{2} = 4$ , is
A $\frac{π}{2}$
B $\frac{π}{3}$
C $\frac{π}{4}$
D $\frac{π}{6}$
Question 3 - Select One
The acute angle between thee lines joining the origin to the points of intersection of the line $\sqrt{3} x + y = 2$ and the circle $x^{2} + y^{2} = 4$ , is
A $\frac{x^{2}}{144} - \frac{y^{2}}{9} = 1$
B $\frac{x^{2}}{169} - \frac{y^{2}}{25} = 1$
C $\frac{x^{2}}{144} - \frac{y^{2}}{25} = 1$
D $\frac{x^{2}}{25} - \frac{y^{2}}{9} = 1$

CENGAGE-CIRCLE -Exercise (Single)

Home
Ask Doubt
Profile