The area bounded by the curves $x^{2} + y^{2} = 1, x^{2} + y^{2} = 4$ and the pair of lines $\sqrt{3} x^{2} + \sqrt{3} y^{2} = 4 x y$ , in the first quadrant is

A

$π / 2$

B

$5 π / 2$

C

$3 π$

D

$π / 4$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:4

The angle $θ$ between the lines represented by
$\sqrt{3} x^{2} - 4 x y + \sqrt{3} y^{2} = 0$ is given by
$θ = {tan}^{- 1} . \frac{\sqrt{h^{2} - a b}}{| a + b |}$
$= {tan}^{- 1} . \frac{2 \sqrt{2^{2} - 3}}{\sqrt{3} + \sqrt{3}} = \frac{π}{6}$
Hence, the shaded area is
$\frac{π / 6}{2 π} \times π (2^{2} - 1^{2}) = \frac{π}{4}$

|

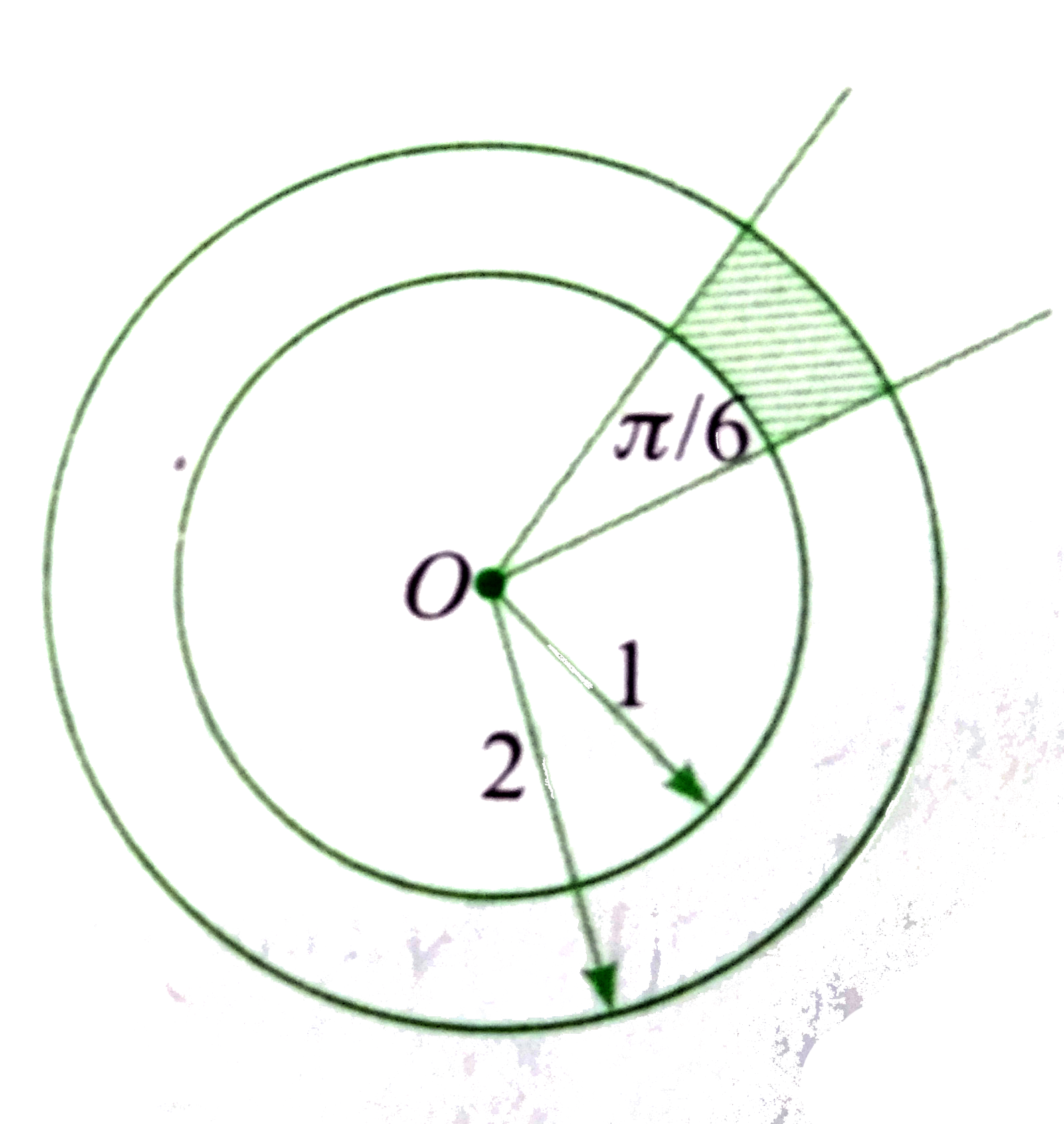
Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The area bounded by the curves $y^{2} = x^{3} and | y | = 2 x$ is
A $\frac{5}{16}$ sq units
B $\frac{16}{5}$ sq units
C $\frac{3}{8}$ sq units
DNone of these
Question 2 - Select One
The area bounded by the curve $y^{2} = 4 x$ and the line $2 x - 3 y + 4 = 0$ is
A $\frac{1}{3}$
B $\frac{2}{3}$
C $\frac{4}{3}$
D $\frac{5}{3}$
Question 3 - Select One
The area bounded by the curves $y = {(x - 1)}^{2}, y = {(x + 1)}^{2} and y = \frac{1}{4}$ is
A $1 / 6$
B $2 / 3$
C $1 / 4$
D $1 / 3$

CENGAGE-CIRCLE -Exercise (Single)

Home
Ask Doubt
Profile