Circle(s) touching x-axis at a distance 3 from the origin and having an intercept of length 2√7 on y-axis is (are)
x2+y2−6x+8y+9=0
x2+y2−6x+7y+9=0
x2+y2−6x−8y+9=0
x2=y2−6x−7y+9=0
The correct Answer is:1,3
The figure shows circles touching the x-axis at A(3,0) and having intercept BD=2sqt(7) on the y-axis.
From the figure, the abscissa of center is 3.
Also, BC= Radius of the circle
=√CM2+BM2=√9+7=4.
Therefore, AC=4
So, the centers of the circles are C(3,4) and C'(3,−4).
Hence, the equations of circles are
(x−3)2+(y±4)20=16
or x2+y2−6x±8y+9=0
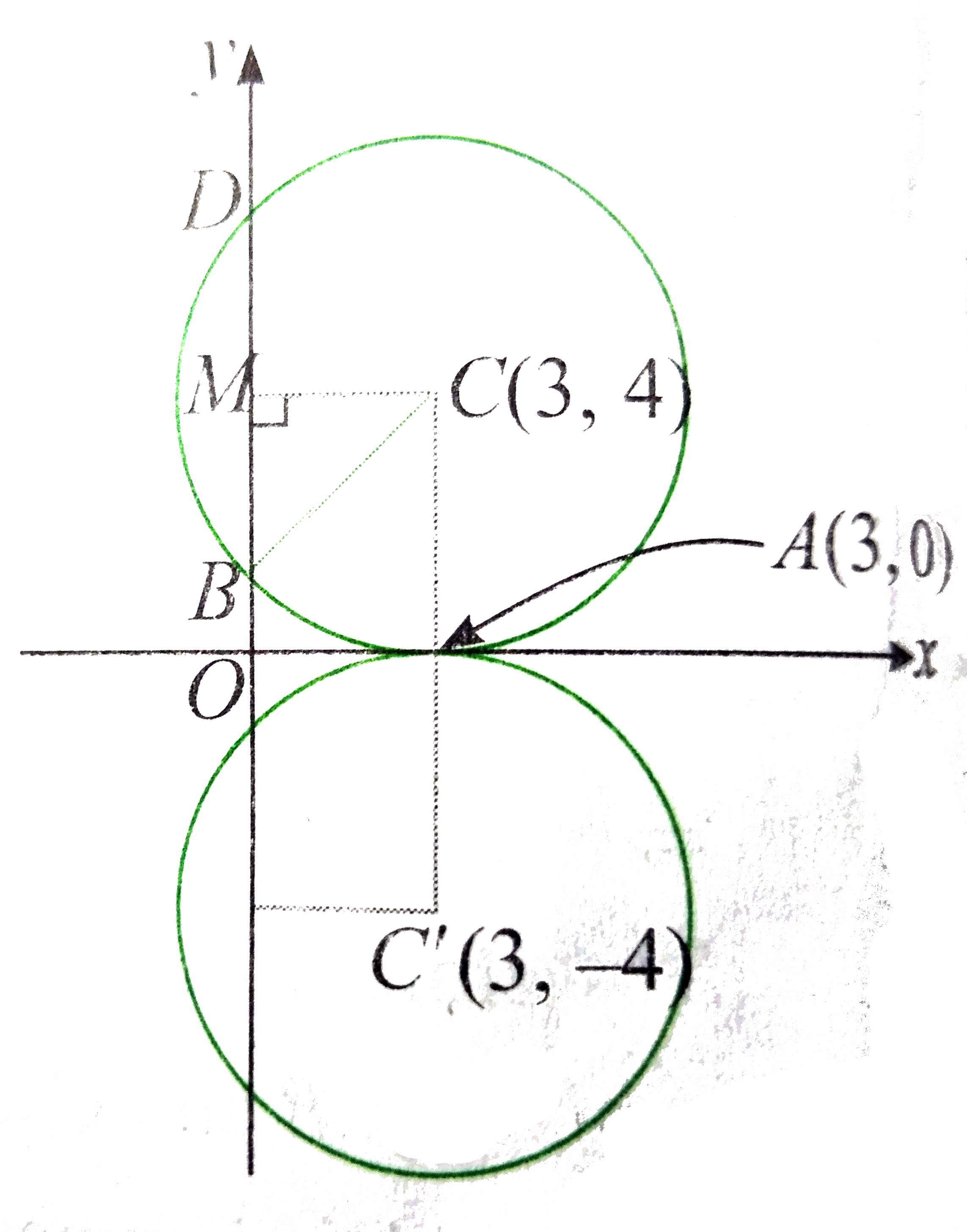
Topper's Solved these Questions
Similar Questions
Knowledge Check
Circle(s) touching x-axis at a distance 3 from the origin and having an intercept of length 2√7 on y-axis is (are)
Ax2+y2−6x+8y+9=0Bx2+y2−6x+7y+9=0Cx2+y2−6x−8y+9=0Dx2+y2−6x−7y+9=0Find the equation of a circle which touches y−aξs at a distance of 4units from the origin and cutsan intercept of 6units along the positive direction of x−aξs.
Ax2+y2+10x−8y+10=0Bx2+y2±10x−8y+16=0Cx2+y2+10x±8y+16=0Dnone
Find the equation of the circle touching the negative y−axis at a distance 5 from the origin and intercepting a length 8 on the x-axis.
View SolutionFind the equation of the circle which touches the axis of y at a distance 4 from the origin and cuts off an intercept of length 6 on the axis of x.
View SolutionFind the equation of a circle which touches y-axis at a distance of 2 units from the origin and cuts an intercept of 3 units with the positive direction of x-axis
View SolutionFind the equation of the a circle which touches y-axis at a distance of 4 units from the origin and cuts an intercept of 6 units along the positive direction of x-axis.
View SolutionFind the equation to the circle which touches the axis of x at a distance+3 from the origin and intercepts a distance 6 on the axis of y
View SolutionFind the equation of a circle which touches y-axis at a distance of 4units from the origin and cuts an intercept of 6units along the positive direction of x-a xis
View Solution