Let RS be the diameter of the circle x2+y2=1, where S is the point (1,0) Let P be a variable a point (other than RandS) on the circle and tangents to the circle at SandP meet at the point Q. The normal to the circle at P intersects a line drawn through Q parallel to RS at point E. then the locus of E passes through the point(s)-
(13,1√3)
(14,12)
(13,−1√3)
(14,−12)
The correct Answer is:1,3
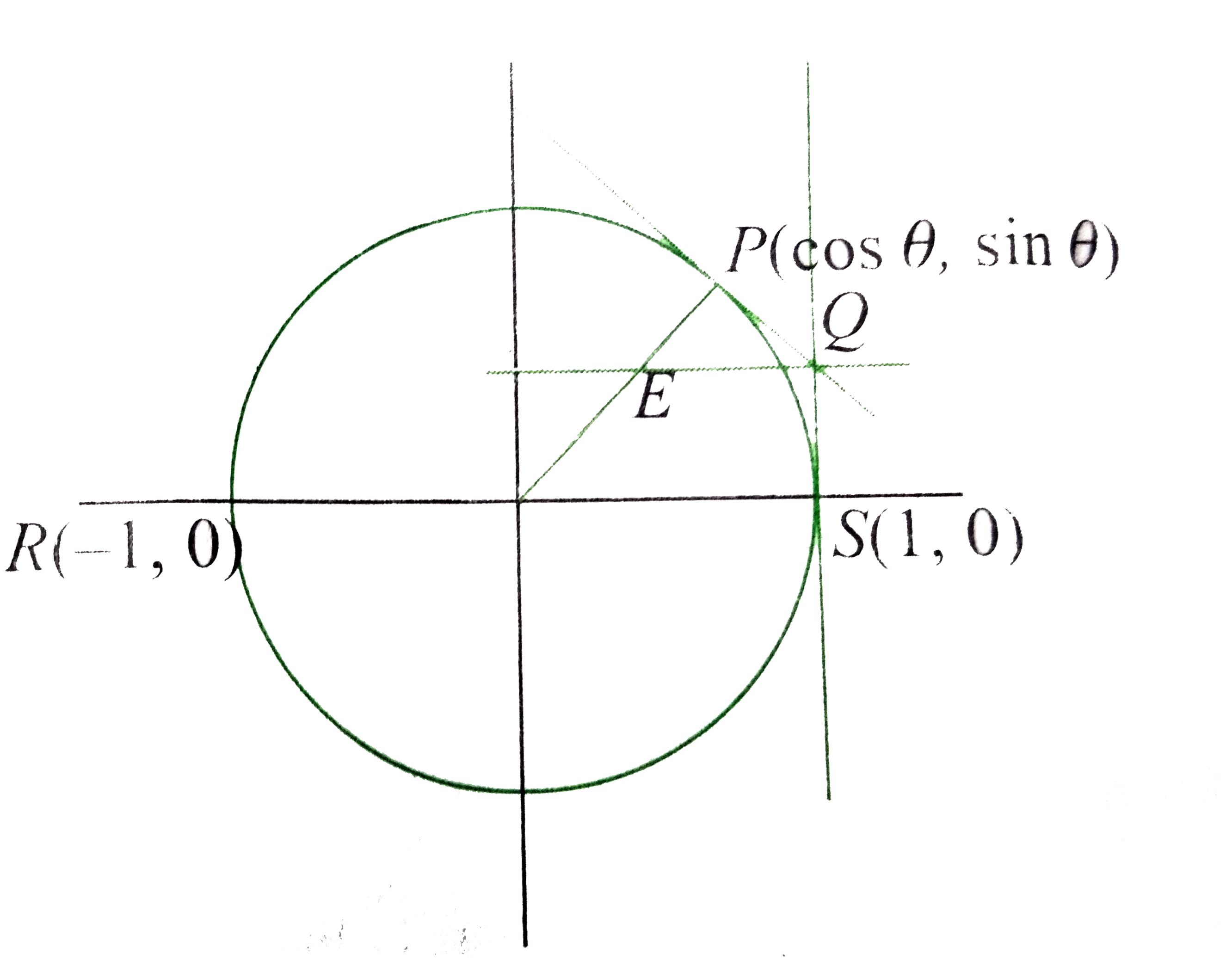
Let point P be (cosθ,sinθ).
Tangent at P is xcosθ+ysinθ=1
∴Q≡(1,1cosθsinθ)
Normal at P,y=tanθx (i)
Equation of QE,y=1−cosθsinθ (ii)
Point E is point of intersection of lines (i) and (ii) .
Eliminating θ from (i) and (ii), we get locus of point E.
From (i) , tanθ=yx
From eq. (ii), we get
y=1−x√x2+y2y√x2+y2=√x2+y2−xy ltbr> or y2+x=√x2+y2
Clearly option (1) and (3) satisfy the above equation.
Topper's Solved these Questions
Similar Questions
Point O is the centre of a circle . Line a and line b are parallel tangents to the circle at P and Q. Prove that segment PQ is a diameter of the circle.

View SolutionIf the tangent to the ellipse x2+2y2=1 at point P(1√2,12) meets the auxiliary circle at point RandQ , then find the points of intersection of tangents to the circle at QandR.
View Solution
Knowledge Check
A tangent to the circle x2+y2=1 through the point (0, 5) cuts the circle x2+y2=4 at P and Q. If the tangents to the circle x2+y2=4 at P and Q meet at R, then the coordinates of R are
A(8√6/5,4/5)B(8√6/5),−4/5)C(−8√6/5),−4/5)Dnone of theseLet P and Q be two points on a circle with centre O. If two tan gents of the circle through P and O meet at A with ∠PAQ=48∘, then ∠APQ is
A96∘B48∘C66∘D60∘Tangents to a circle at points P and Q on the circle intersect at a point R. If PQ= 6 and PR= 5 then the radius of the circle is
A133B4C154D165
If the normal to the parabola y2=12x at the point P(3,6) meets the parabola again at the point Q,then equation of the circle having PQ as a diameter is
View Solutionif P is a variable point and PQ and PRare the tangent drawn to the circle x2+y2=9. Let QR be always touching the circle x+y2=4, then locus of P is
View SolutionThe tangent at any point to the circle x2+y2=r2 meets the coordinate axes at A and B.If the lines drawn parallel to axes through A and B meet at P then locus of P is
View SolutionIf a tangent to the circle x2+y2=1 intersects the coordinate axes at distinct points P and Q, then the locus of the mid-point of PQ is :
View SolutionIf a tangent to the circle x2+y2=1 intersects the coordinate axes at distinct point P and Q. then the locus of the mid- point of PQ is
View Solution
