In right triangle ABC, right angle is at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that :
(i)ΔAMC≅ΔBMD
(ii)∠DBC is a right angle
(iii)ΔDBC≅ΔACB (iv)CM=12AB.
 Solution in Tamil
Solution in Tamil
Step by step video & image solution for In right triangle ABC, right angle is at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that : (i) DeltaAMC ~= DeltaBMD (ii) /_DBC is a right angle (iii) Delta DBC ~= DeltaACB (iv)CM = 1/2 AB. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILAR TRIANGLES BOOK - NCERT TAMILCHAPTER - SIMILAR TRIANGLES EXERCISE - EXERCISE - 8.3
6 Videos
- SIMILAR TRIANGLES BOOK - NCERT TAMILCHAPTER - SIMILAR TRIANGLES EXERCISE - EXERCISE - 8.4
14 Videos
- SIMILAR TRIANGLES BOOK - NCERT TAMILCHAPTER - SIMILAR TRIANGLES EXERCISE - EXERCISE - 8.1
9 Videos
- SETSBOOK - NCERT TAMILCHAPTER - SETSEXERCISE - Try This
9 Videos
- STATISTICSBOOK - NCERT TAMILCHAPTER - STATISTICSEXERCISE - THINK AND DISCUSS
8 Videos
Similar Questions
In trigle ABC, the points D, E, F are the midpoints of the sides BC,CA, and AB respee. Tively. Using vector methed ,show that the area of Δ DEF is equal to 14 (area of ABC).
View SolutionProve that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals
View SolutionIn ΔPQR, ST is a line such that PSSQ=PTTR and also ∠PST=ΔPRQ.
Prove that ΔPQR is an isosceles triangle .

View SolutionWrite some sets of your choice, involving algebraic and geometrical ideas.
View SolutionThe mean value can be calculated from both ungrouped and grouped data. Which one do you think is more accurate? Why?
View SolutionIn right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:
(i) ΔAMC≅ΔBMD
(ii) ∠DBC is a right angle
(iii) ΔDBC≅ΔACB
(iv) CM=12AB

View Solutionएक समकोण त्रिभुज ABC में, जिसमें कोण C समकोण है, M कर्ण AB का मध्य-बिंदु है। C को M से मिलाकर D तक इस प्रकार बढ़ाया गया है कि DM = CM है। बिंदु D को बिंदु B से मिला दिया जाता है। दर्शाइए कि
(i) ΔAMC≅ΔBMD
(ii) ∠DBC एक समकोण है
(iii) ΔDBC≅ΔACB
(iv) CM=12AB

View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B. Show that
(i) △AMC≅△BMD
(ii) ∠DBC is a right angle.
(iii) △DBC≅△ACB
(iv) CM=12AB

View SolutionIn right triangle ABC, right angle is at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that :
(i)ΔAMC≅ΔBMD
(ii)∠DBC is a right angle
(iii)ΔDBC≅ΔACB (iv)CM=12AB.
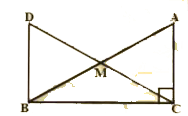
View SolutionIn right triangle ABC, right angle is at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that :
(i)ΔAMC≅ΔBMD
(ii)∠DBC is a right angle
(iii)ΔDBC≅ΔACB (iv)CM=12AB.
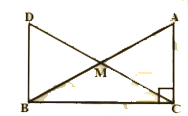
View SolutionIn right triangle ABC, right angle is at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that :
(i)ΔAMC≅ΔBMD
(ii)∠DBC is a right angle
(iii)ΔDBC≅ΔACB (iv)CM=12AB.
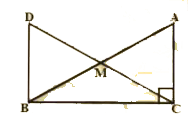
View SolutionIn right triangle ABC, right angle is at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that :
(i)ΔAMC≅ΔBMD
(ii)∠DBC is a right angle
(iii)ΔDBC≅ΔACB (iv)CM=12AB.
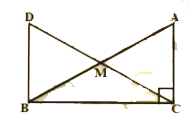
View SolutionIn right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:
(i) ΔAMC≅ΔBMD
(ii) ∠DBC is a right angle
(iii) ΔDBC≅ΔACB
(iv) CM=12AB

View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.
 ) Show that : ΔAMC≅ΔBMD.
) Show that : ΔAMC≅ΔBMD.
View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.
 ) Show that : ∠DBC is a right angle.
) Show that : ∠DBC is a right angle.
View SolutionIn right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (See Fig.
 ) Show that : ΔDBC≅ΔACB.
) Show that : ΔDBC≅ΔACB.
View Solution
