‘O’ is any point in the interior of a triangle ABC. If OD⊥BC,OE⊥AC and OF ⊥ AB, show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BE2.
 Solution in Tamil
Solution in Tamil
Step by step video & image solution for ‘O’ is any point in the interior of a triangle ABC. If OD bot BC, OE botAC and OF bot AB, show that (i) OA^(2) + OB^(2) + OC^(2) - OD^(2) - OE^(2) - OF^(2) = AF^(2) + BD^(2) + CE^(2) (ii) AF^(2) + BD^(2) + CE^(2) = AE^(2) + CD^(2) + BE^(2). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILAR TRIANGLES BOOK - NCERT TAMILCHAPTER - SIMILAR TRIANGLES EXERCISE - OPTIONAL EXERCISE
6 Videos
- SIMILAR TRIANGLES BOOK - NCERT TAMILCHAPTER - SIMILAR TRIANGLES EXERCISE - TRY THIS
5 Videos
- SIMILAR TRIANGLES BOOK - NCERT TAMILCHAPTER - SIMILAR TRIANGLES EXERCISE - EXERCISE - 8.3
6 Videos
- SETSBOOK - NCERT TAMILCHAPTER - SETSEXERCISE - Try This
9 Videos
- STATISTICSBOOK - NCERT TAMILCHAPTER - STATISTICSEXERCISE - THINK AND DISCUSS
8 Videos
Similar Questions
In the given figure,
QTPR=QRQSand∠1=∠2
Prove that ΔPQS~ΔTQR.

View SolutionIn triangle ΔPQR, E and F are points on the sides PQ and PR respectively. State whether EF ||QR or not?
(i) PE = 3.9 cm EQ = 3 cm PF = 3.6 cm and FR = 2.4 cm
View SolutionIn trigle ABC, the points D, E, F are the midpoints of the sides BC,CA, and AB respee. Tively. Using vector methed ,show that the area of Δ DEF is equal to 14 (area of ABC).
View SolutionWrite some sets of your choice, involving algebraic and geometrical ideas.
View SolutionThe mean value can be calculated from both ungrouped and grouped data. Which one do you think is more accurate? Why?
View Solutionआकृति 6 . 54 में ΔABC के अभ्यन्तर में स्थित कोई बिंदु O है तथा OD⊥BC,OE⊥AC और OF⊥AB है दर्शाइए कि
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BF2
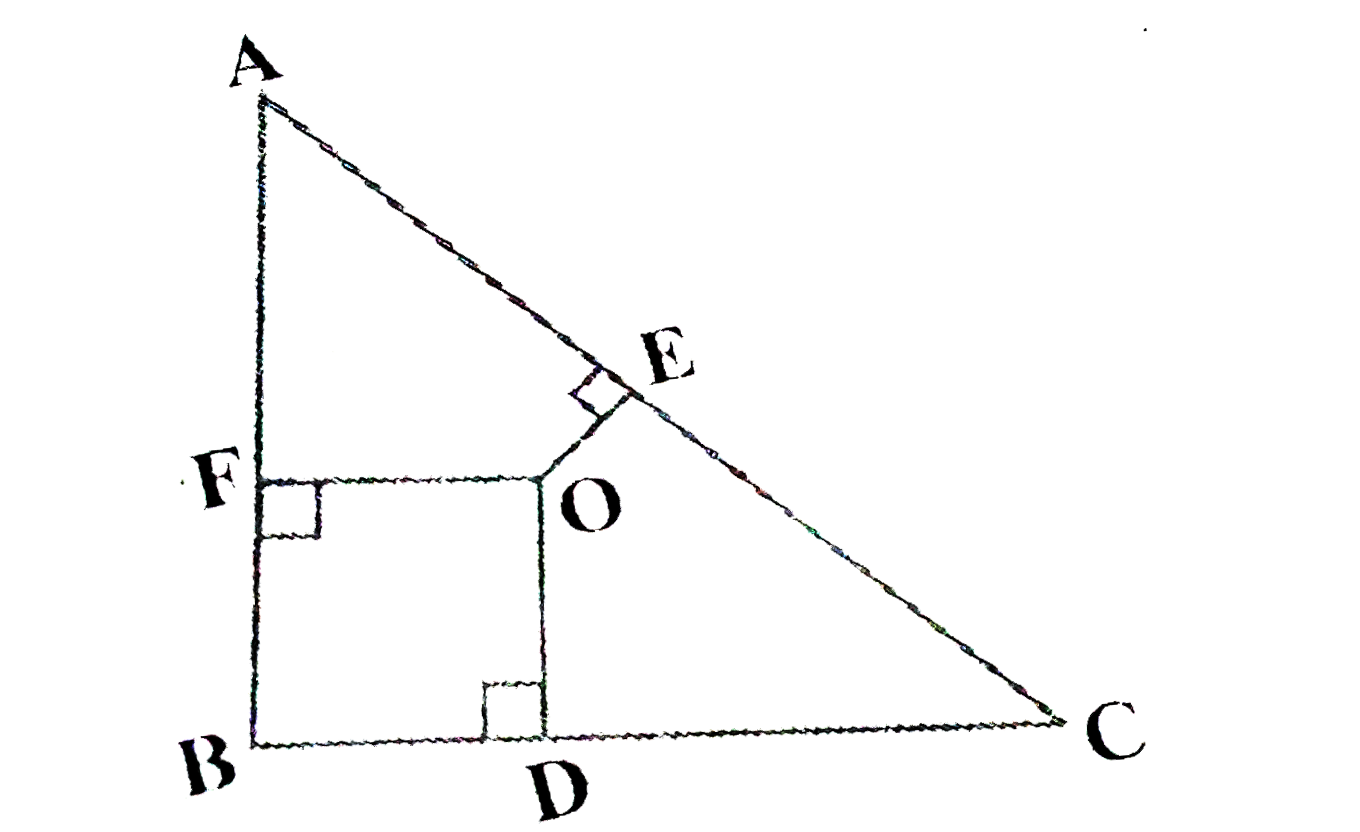
View SolutionO is a point in the interior of ΔABC,OD⊥BC,OE⊥ACandOF⊥AB, as shown in the figure,
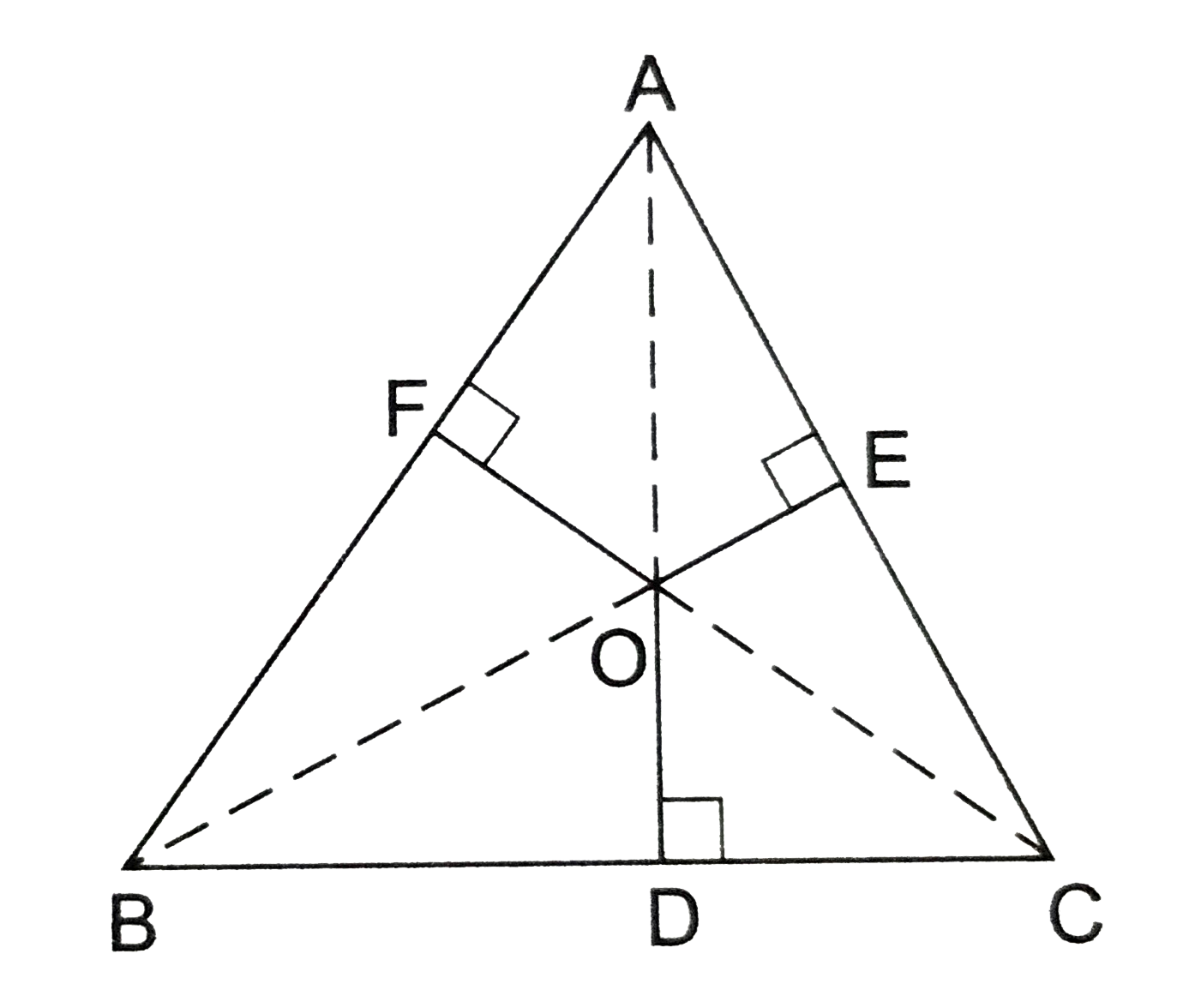
Prove that :
(i)OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AD2+BF2+CD2
View SolutionΔABC के अंदर बिंदु O से भुजाओ BC,CA और AB पर क्रमश: लंब OD,OE और OF डाले गए है। सिद्ध कीजिए कि
AF2+BD2+CE2=OA2+OB2+OC2−OD2−OE2−OF2.
View SolutionIn Fig. 2.54, o is a point in the interior of a triangle ABC,OD⊥BC,OE⊥ACandof⊥AB. Show that
OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2,
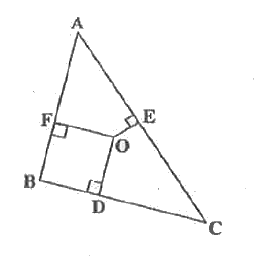
View SolutionIn fig . O is a point in the interior of a triangle ABC , OD ⊥BC,OE⊥ACandOF⊥AB . Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2+AE2+CD2+BF2 .
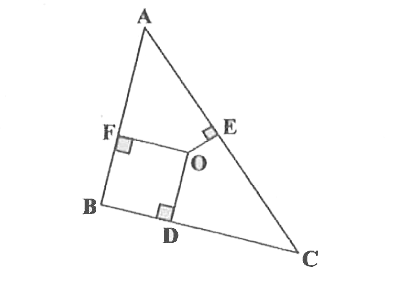
View Solutionआकृति में , ΔABC के अभ्यंतर में स्थित कोई बिंदु O है तथा OD⊥BC , OE⊥AC और OF⊥AB है । दर्शाइए कि
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BF2 .
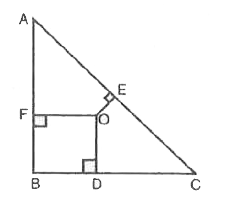
View Solutionత్రిభుజము ABC అంతరంలో ఏదైనా బిందువు 'O' OD⊥BC,OE⊥AC మరియు OF⊥AB అయిన OA2+OB2+OC2−OD2−OE2−OE2=AE2+BD2+CE2
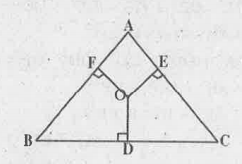
View Solutionత్రిభుజము ABC అంతరంలో ఏదైనా బిందువు 'O' OD⊥BC,OE⊥AC మరియు OF⊥AB అయిన AE2+BF2+CD2=AF2+BD2+CE2 అని చూపండి.
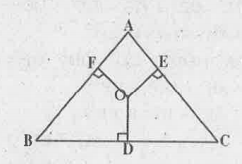
View Solution‘O’ is any point in the interior of a triangle ABC. If OD⊥BC,OE⊥AC and OF ⊥ AB, show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BE2.
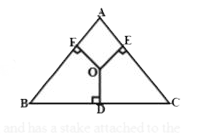
View Solution‘O’ is any point in the interior of a triangle ABC. If OD⊥BC,OE⊥AC and OF ⊥ AB, show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BE2.
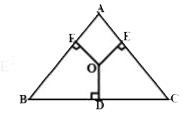
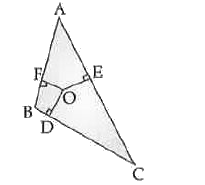
View SolutionIn the figure given below, O is point in the interior of a triangle ABC, OD⊥BC, OE⊥AC and OF⊥AB. Show that
(i) OA2+OB2+OC2+OD2−OE2−OF2=AR2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BF2
View Solution
