In ΔABC,D is the midpoint of BC. If DL⊥AB and DM⊥AC such that DL = DM, prove that AB = AC.
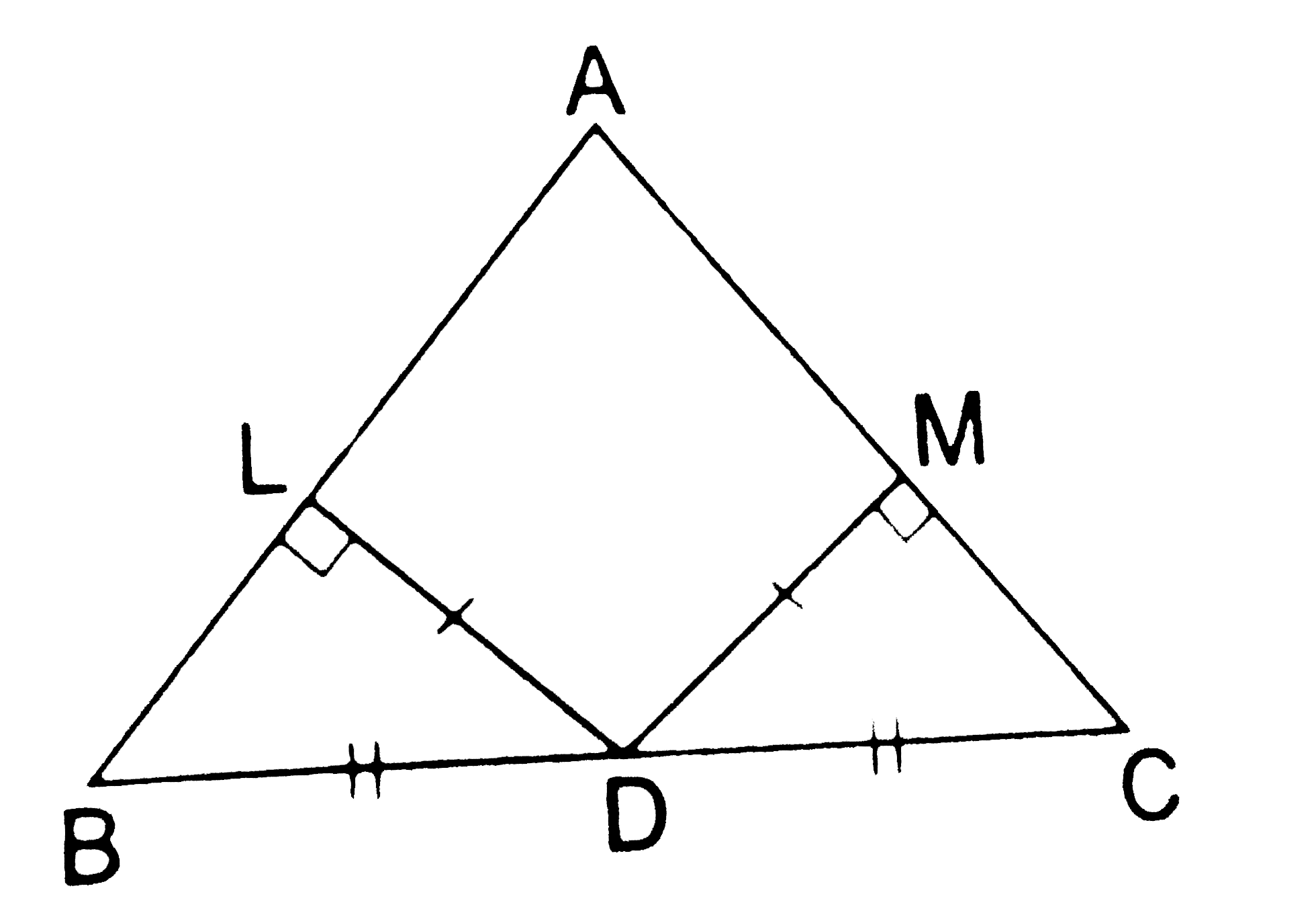
ΔBDL≅ΔCDM as BD=CD,DL=DM,∠BLD=∠CMD=90∘.
∴ ∠B=∠Cand hence AB=AC.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B16videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)20videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)20videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)37videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)22videos
COORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
In △ABC ,∠A=90∘. M is the midpoint of BC and D is a point on BC such that AD⊥BC. If AB= 7 cm and AC = 24 cm, then AD:AM is equal to:
△ABC में, ∠A=90∘ है, M, BC का मध्य बिंदु है तथा D, BC पर स्थित ऐसा बिंदु है कि AD⊥BC है | यदि AB= 7 सेमी, AC = 24 सेमी है, तो AD:AM किसके बराबर है ?A168:275B336:625C24:25D32:43 - Question 2 - Select One
In triangle ABC,D is the midpoint of AB, E is the midpoint of DB and F is the midpoint of BC. If the area of ΔABC is 96, the area of ΔAEF is
A16B24C32D36
In ΔABC , if L and M are the points on AB and AC, respectively such that LM∣∣BC. Prove that ar(ΔLOB)=ar(ΔMOC).
View SolutionIn ΔABC,DandE two points on AB such that AD=BE. If DP||BCandEQ||AC, prove that such PQ∣∣AB.
 View Solution
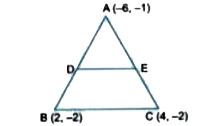
View SolutionIn the given Fig. 3, in ΔABC,DandE are the mid point of the sides AB and AC respectively. Find the length of DE. Prove that DE=12BC.
 View Solution
View SolutionABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
View SolutionIn the given figure C is the midpoint of AB,D is the midpoint of XY and AC=XD Using an Euclid 's axiom prove that AB =XY
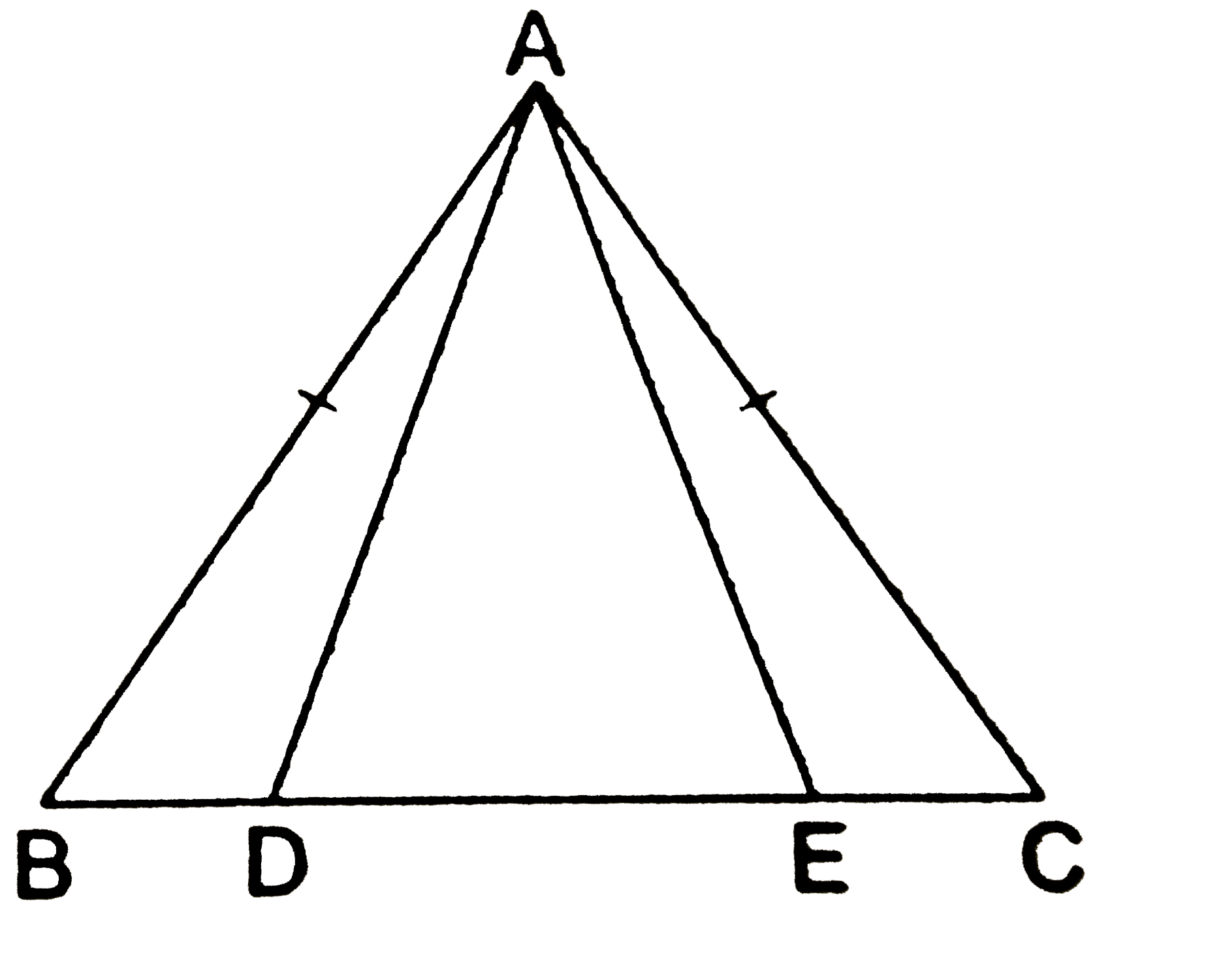
View SolutionIn an isosceles ΔABC with AB = AC, D and E are point on BC such that BE = CD. Show that AD = AE.
 View Solution
View Solution

