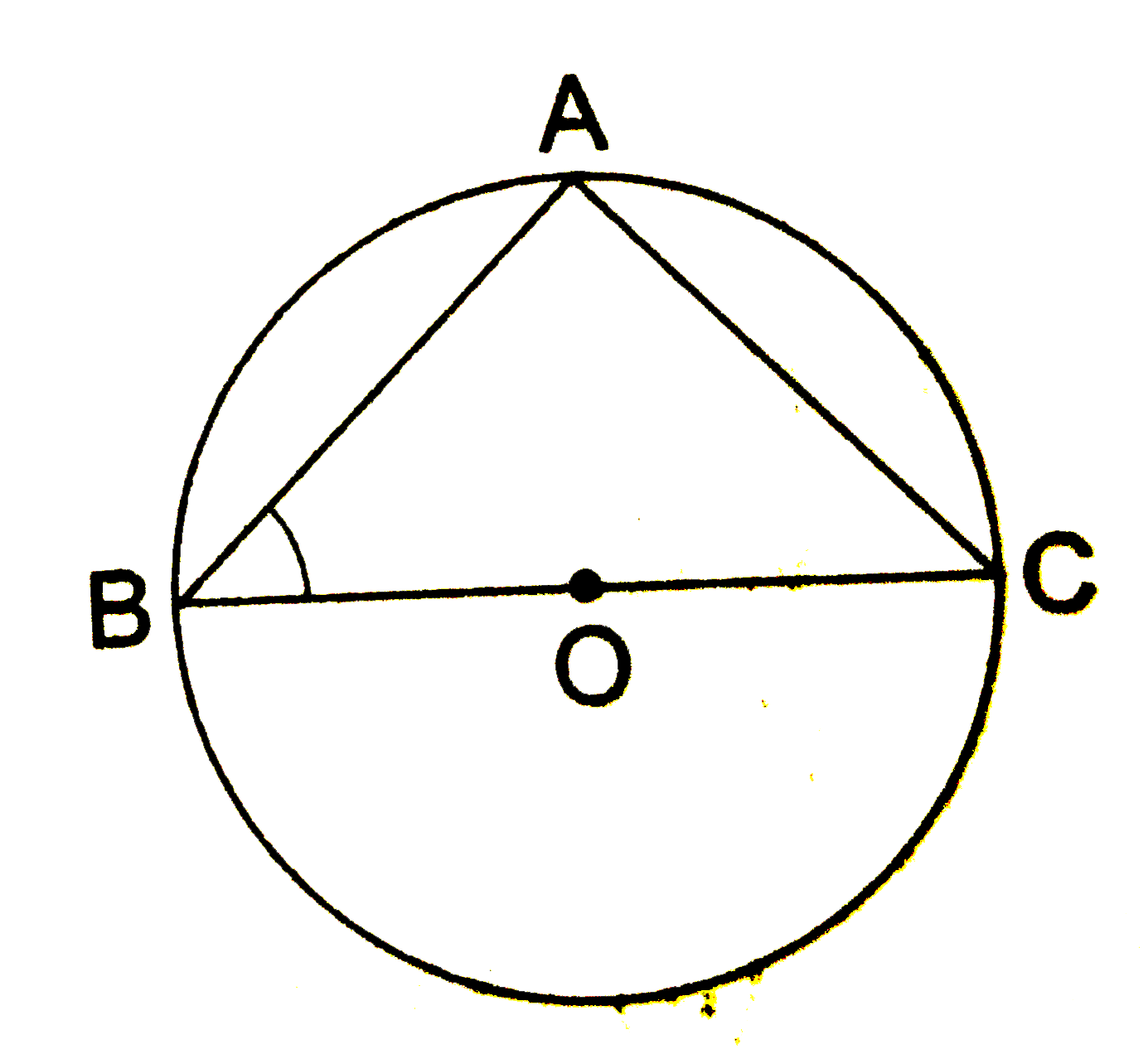
In the given figure, BOC is a diameter of a circle and AB=AC . Then , ∠ABC=?
A
30∘
B
45∘
C
60∘
D
90∘
Video Solution
Text Solution
The correct Answer is:B
Since an angle in a semicircle is a right angle ∠BAC=90∘
∴∠BAC+∠ACB=90∘
Now, AB=AC⇒∠ABC=∠ACB=45∘
|
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Multiple Choice Questions (Mcq)
5 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
In the given figure, AB is the diameter of the circle. Find the value of ∠ACD:
 A30∘B60∘C45∘D25∘
A30∘B60∘C45∘D25∘In the given figure, AC is a diameter of a circle with radius 5 cm. if AB=BC and CD=8 cm, the area of the shaded region to the nearest whole number is
 A28 cm2B29 cm2C30 cm2D45 cm2
A28 cm2B29 cm2C30 cm2D45 cm2In the given figure, AB is the diameter of the circle, ∠ADC=120∘. Find ∠CAB:
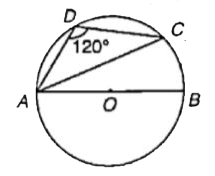 A20∘B30∘C40∘Dcan't be determined
A20∘B30∘C40∘Dcan't be determined
If the given figure, AB is diameter of the circle, C and D lie on the semicircle. ∠ABC=65∘and∠CAD=45∘, find ∠DCA.
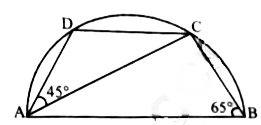
View SolutionIn the given figure, AB=AC. prove that :
View SolutionIn the given figure O is the centre of the circle and AB is a tangent at B. If AB=15 cm and AC=7.5 cm, find the rdius of the circle.

View Solution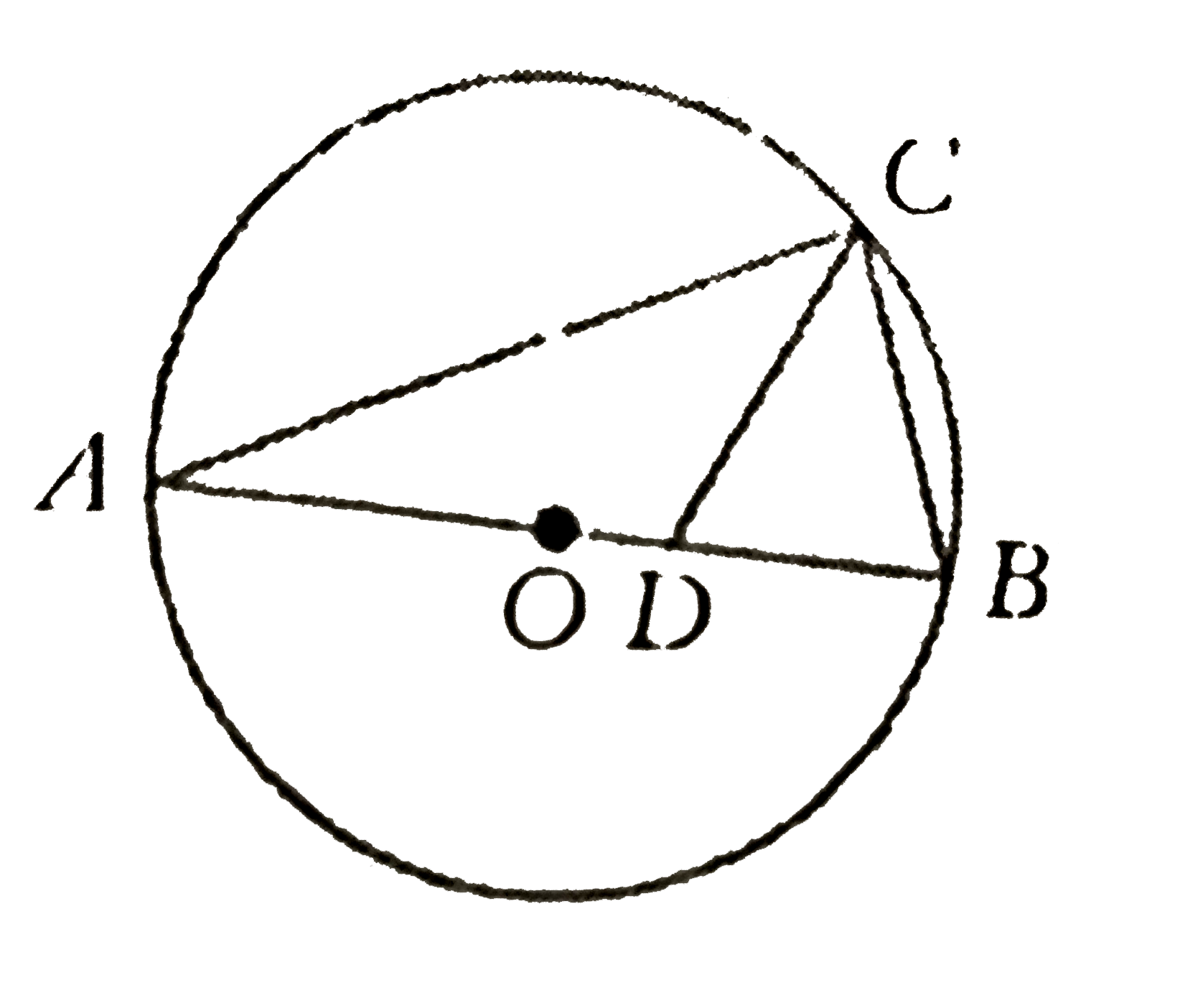
In the given figure, AB is the diameter and ∠ADC=2∠BDC. If ∠BCD=70∘, then find the angle made by AC at the centre of the circle.
View SolutionIn the given figure, ∠COB=40∘,AB is the diameter of the circle. Find m∠CAB:

View Solution
