If the altitudes from two vertices of a triangle to the opposite sides are equal, prove that the triangle is isosceles.
equilateral
isosceles
scalene
right angled
The correct Answer is:B
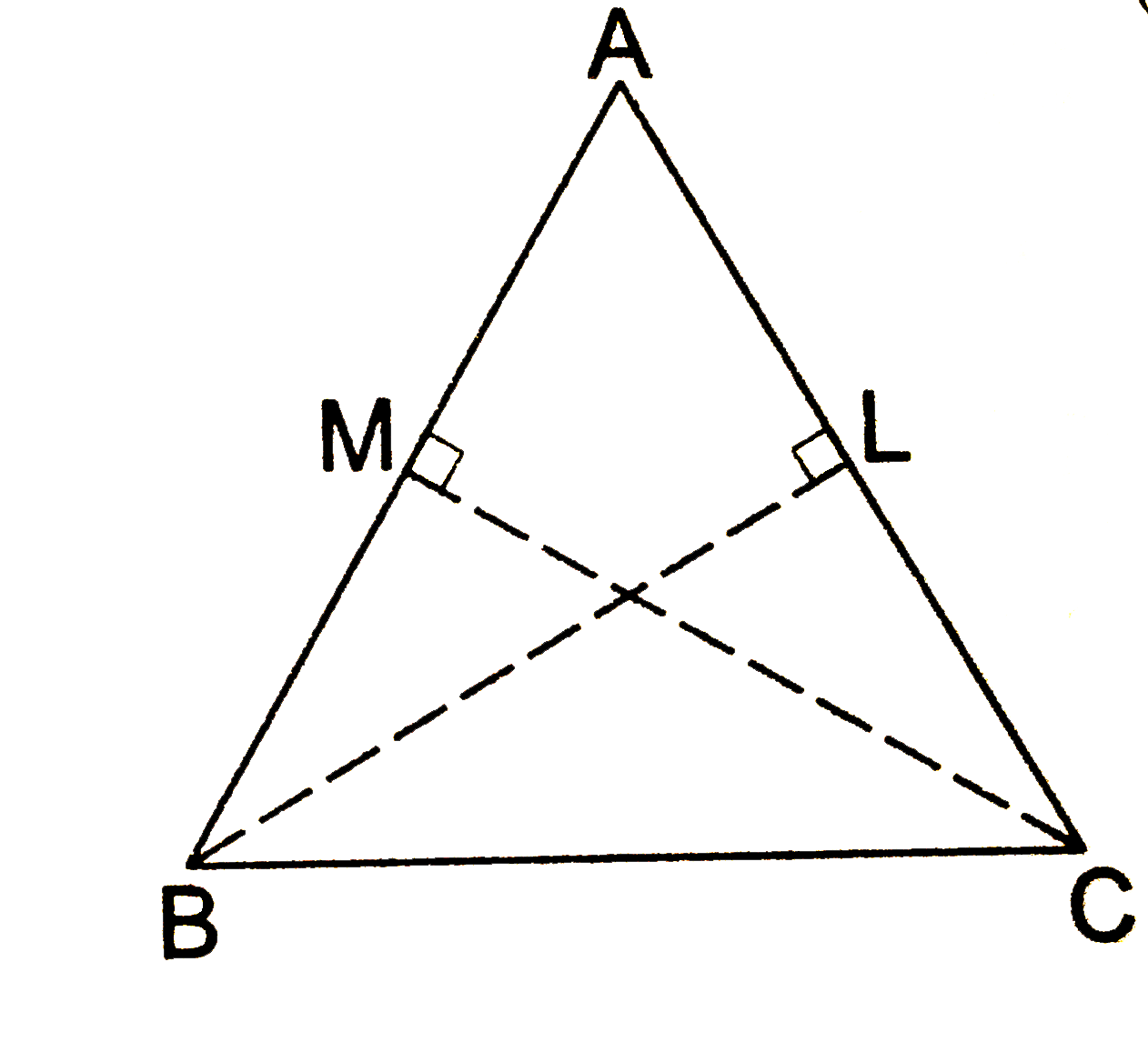
A ΔABC is given in which BL⊥AC and CM⊥AB such that BL = CM. Then, we have to prove that AB = AC.
In ΔABL and ΔACM, we have :
BL = CM (given)
∠BAL=∠CAM(common),
∠ALB=∠AMC(each 60∘)
ΔABL≅ΔACM and hence AB=AC.
ΔABC is isosceles.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B16videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)37videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)22videos
COORDINATE GEOMETRY
Similar Questions
If the altitude from one vertex of a triangle bisects the opposite side, then the triangle is isosceles. GIVEN : A ABC such that the altitude AD from A on the opposite side BC bisects BC i.e., BD=DC. TO PROVE : AB=AC i.e. the triangle ABC is isosceles.
View SolutionWhich of the following statements are true (T) and which are false (F): Side opposite to equal angles of a triangle may be unequal. Angle opposite to equal sides of a triangle are equal. The measure of each angle of an equilateral triangle is 600. If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles. The bisectors of two equal angles of a triangle are equal. If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles. The two altitudes corresponding to two equal sides of a triangle need not be equal. If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent. Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal to the hypotenuse and a side of the other triangle.
View SolutionIf the bisector of an angle of a triangle bisects the opposite side, prove that the triangle is isosceles.
View SolutionIf the altitude from one vertex of a triangle bisects the opposite side; then the triangle is isosceles.
View SolutionIf the bisector of the vertical angle of a triangle bisects the base, prove that the triangle is isosceles.
View SolutionThe bisectors of the angles B and C of a triangle ABC , meet the opposite sides in D and E respectively. If DE||BC , prove that the triangle is isosceles.
View SolutionAltitudes the perpendiculars drawn from the vertices of a triangle to the opposite side are known as the altitudes of the triangle.
View SolutionThe length of the altitudes from the vertices A,B,C of a triangle ABC to opposite sides are 24,18,725 respectively. If Δ is the area of the triangle ABC then 3√Δ is equal to
View SolutionBE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
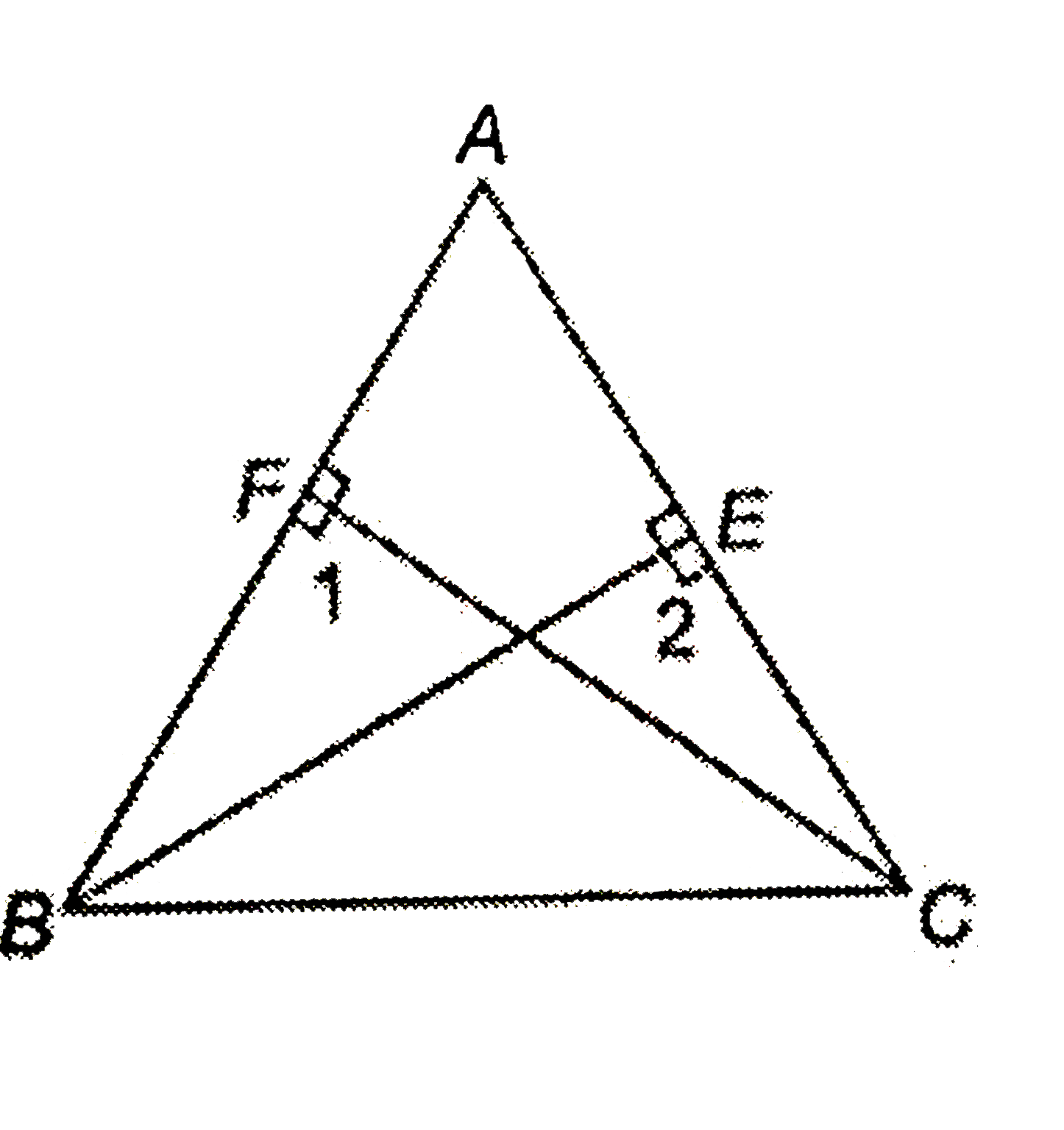 View Solution
View SolutionBE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
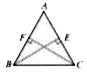 View Solution
View Solution

