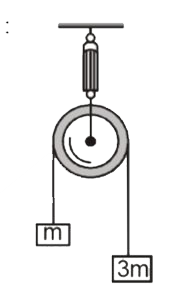
In the system shown, the masses are released from rest. What shall be the acceleration of the moving masses?
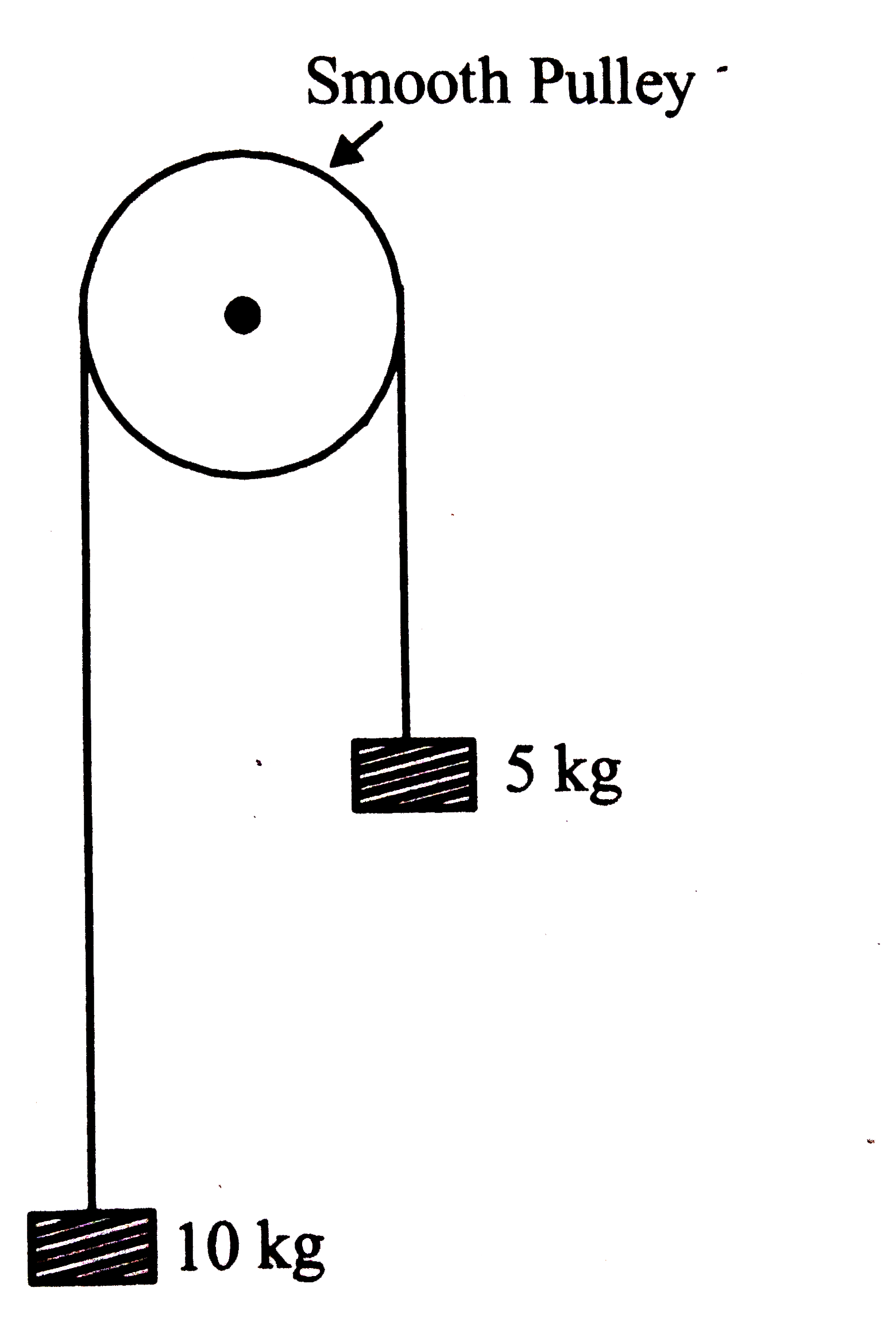
g
2g/3
g/3
g/2
The correct Answer is:C

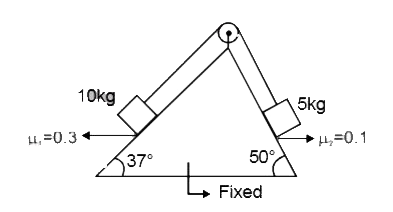
For 10 kg mass
10g−T=10a (i)
For 5 kg mass
T−5g=5a (ii)
From (i) and (ii), we get
a=5g15=g3
Topper's Solved these Questions
Similar Questions
In the system shown in figure, the block A is released from rest. Find
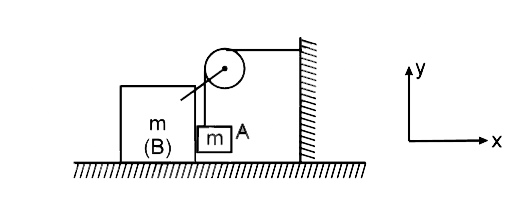
the acceleration of both blocks ‘A’ and ‘B’.
View SolutionIn the system shown in the figure all surfaces are smooth, pulley and string are massless. The string between the two pulleys and between pulley and block of mass 5 m is parallel to the incline surface of the block of mass 4 m. The system is released from rest. Find the acceleration of the block of mass 4 m . [tan37∘=34]
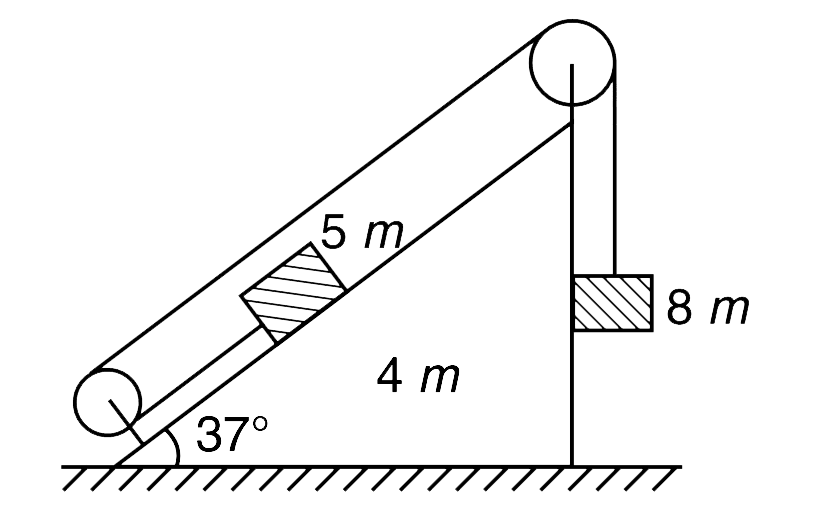
View Solution
Knowledge Check
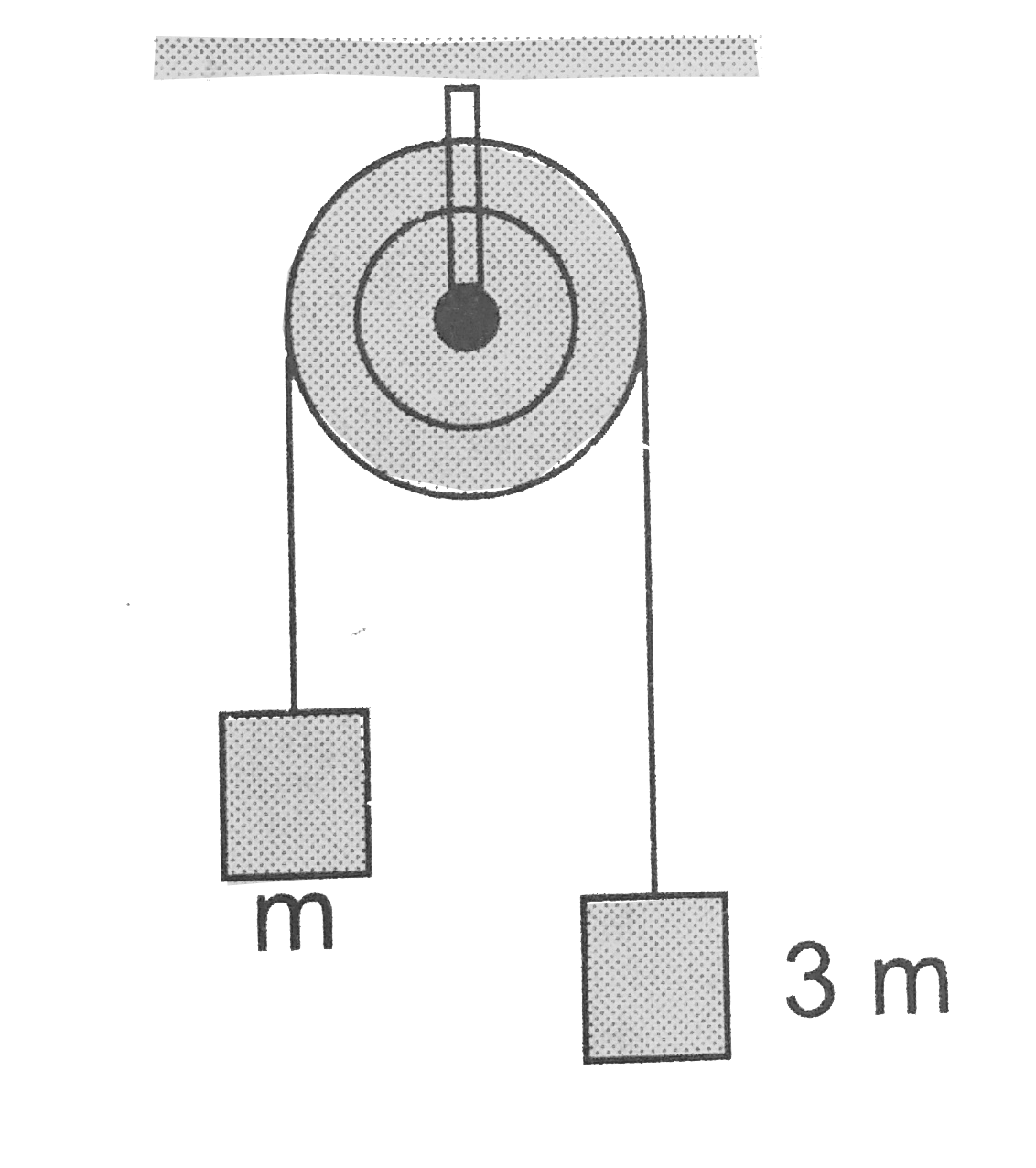
In the system given below ,the masses are relased from rest

What shall be acceleration of the moving masses ?AgB2g/3Cg/3Dg/2Two masses (M+m)and(M−m) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are released from rest, the acceleration of the system is
Agm/MB2gM/mCgm/2MDg(M2−m2)/2MIn the system shown block is released from rest on the inclined surface of the wedge. The acceleration of the wedge will be (assume friction to be absent)
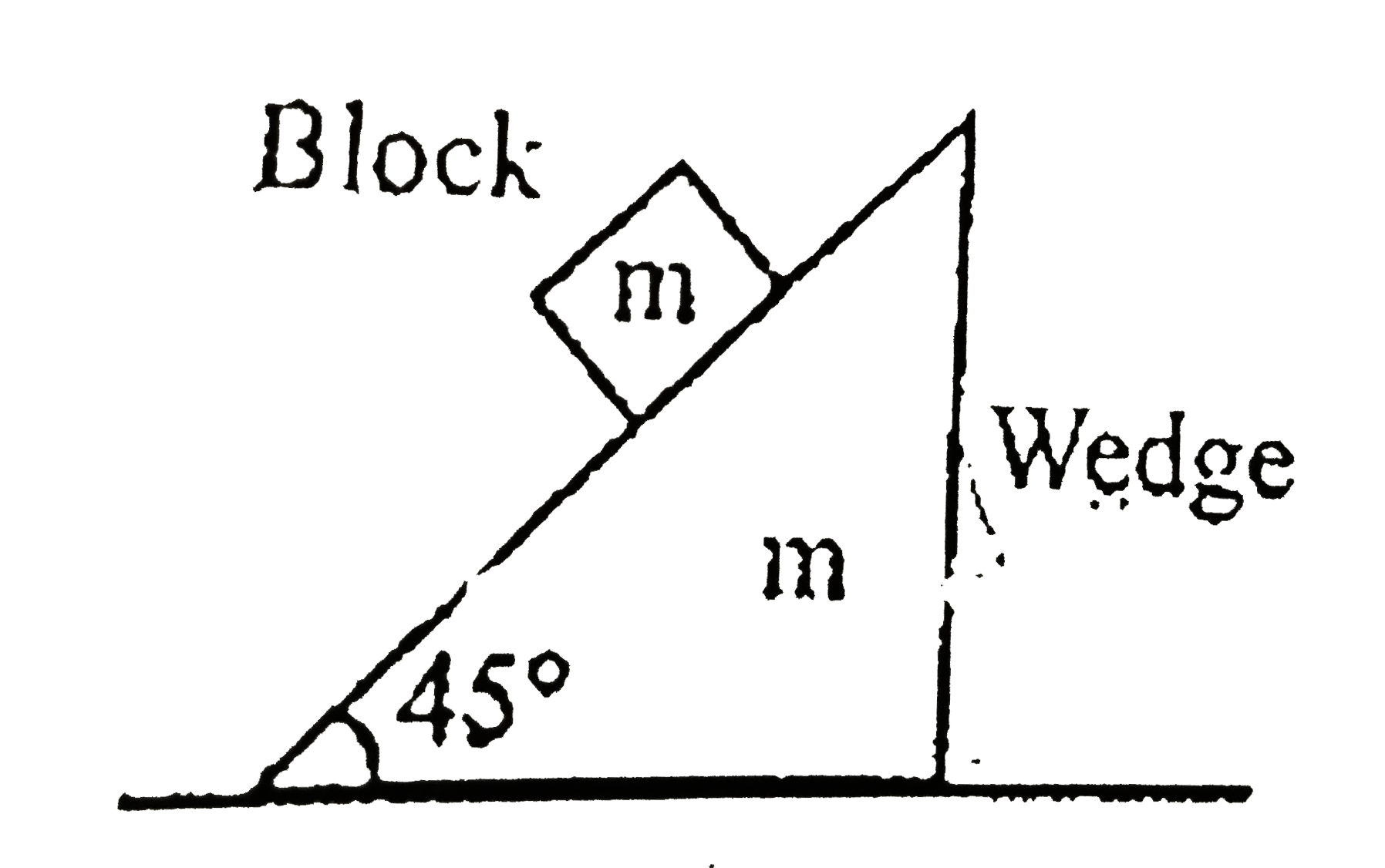 Ag5Bg4Cg3Dg2
Ag5Bg4Cg3Dg2
Two blocks of masses 5kg and 10kg are attached with the help of light string and placed on a rough incline as shown in the figure. Coefficients of friction are as marked in the figure. The system is released from rest. Determine the acceleration of the two blocks.
View SolutionIf the system is released, then the acceleration of the centre of mass of the system :
View SolutionIn the arrangement shown, the blocks of unequal masses are held at rest. When released, acceleration of the blocks is

View SolutionIf the system is released, then the acceleration of the centre of mass of the system is :
 .
.
View SolutionAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses 'm'and '2m' are placed as shown in Fig. There is no friction anywhere. A spring of force constant k is attached to the bigger block. Mass 'm' is kept in touch with the spring but not attached to it. 'A' and 'B' are two supports attached to '2m'. Now m is moved towards left so that spring is compressed by distance 'x' and then the system is released from rest.

What is the loss in the energy of the system due to breaking of B?
View Solution
