A mass m1 is moving on a plane surface along a straight path under the action of a force F. Another mass m2 is added on to m1 and the acceleration drops to 1/5 of the ear her value of the acceleration. Assuming that F remains constant, what is the ratio m1:m2 ?
1/6
1/5
1/4
4/5
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Understand the initial conditions
Let the initial mass be m1 and the initial acceleration be a. The force acting on the mass is given by Newton's second law:
F=m1⋅a
Step 2: Understand the conditions after adding the second mass
When a second mass m2 is added to the first mass, the new total mass becomes m1+m2. The new acceleration, as per the problem, is 15 of the initial acceleration:
a′=a5
Step 3: Write the equation for the new conditions
Since the force F remains constant, we can write the equation for the new situation:
F=(m1+m2)⋅a′
Substituting a′ into the equation gives:
F=(m1+m2)⋅a5
Step 4: Set the two expressions for force equal to each other
Since both expressions represent the same force F, we can equate them:
m1⋅a=(m1+m2)⋅a5
Step 5: Simplify the equation
To eliminate a from both sides (assuming a≠0), we can divide both sides by a:
m1=(m1+m2)⋅15
Step 6: Multiply through by 5 to eliminate the fraction
Multiplying both sides by 5 gives:
5m1=m1+m2
Step 7: Rearrange the equation to find m2
Rearranging the equation gives:
5m1−m1=m2
4m1=m2
Step 8: Find the ratio m1:m2
Now, we can express the ratio m1m2:
m1m2=m14m1=14
Thus, the ratio m1:m2 is:
m1:m2=1:4
Final Answer
The ratio m1:m2 is 1:4.
---
Let the initial mass be m1 and the initial acceleration be a. The force acting on the mass is given by Newton's second law:
F=m1⋅a
When a second mass m2 is added to the first mass, the new total mass becomes m1+m2. The new acceleration, as per the problem, is 15 of the initial acceleration:
a′=a5
Since the force F remains constant, we can write the equation for the new situation:
F=(m1+m2)⋅a′
Substituting a′ into the equation gives:
F=(m1+m2)⋅a5
Since both expressions represent the same force F, we can equate them:
m1⋅a=(m1+m2)⋅a5
To eliminate a from both sides (assuming a≠0), we can divide both sides by a:
m1=(m1+m2)⋅15
Multiplying both sides by 5 gives:
5m1=m1+m2
Rearranging the equation gives:
5m1−m1=m2
4m1=m2
Now, we can express the ratio m1m2:
m1m2=m14m1=14
m1:m2=1:4
The ratio m1:m2 is 1:4.
Topper's Solved these Questions
Similar Questions
Figure-2.57 shows a large block of mass M, supporting two small mass m1 and m2, connected by a light, frictionless thread. A force F is acting on M, such that the block m1 is sliding down, with an acceleration a1. Find the force F applied on M and also the acceleration of M. Assuming all surfaces are frictionless.
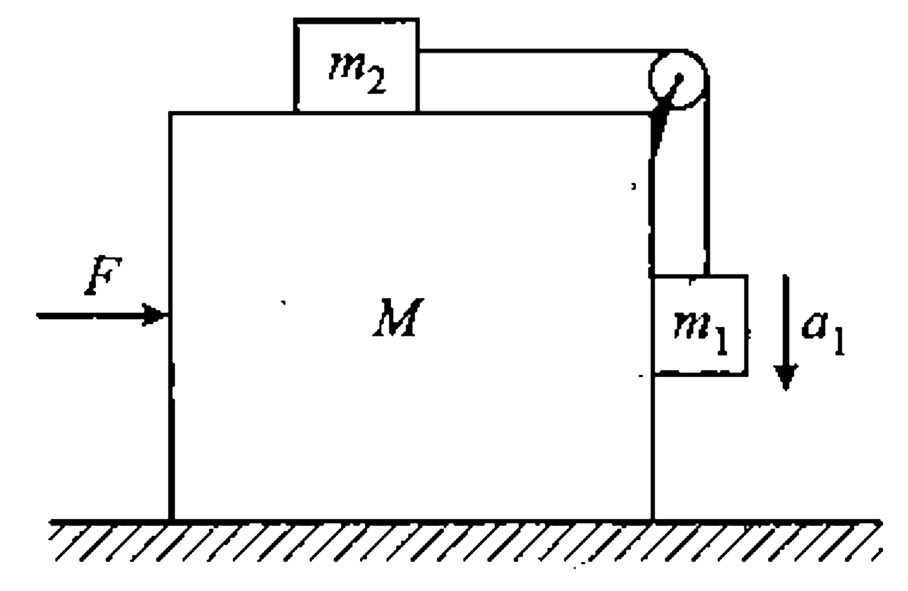
View SolutionA body A mass m1 exerts a force on another body B of mass m2 . If the acceleration of B be a2 , then the acceleration (in magnitude) of A is
View Solution
Knowledge Check
A particle of mass M moves with constant speed along a circular path of radius r under the action of a force F. Its speed is
A√rFmB√FrC√FmrD√FmrIn the figure shown, the acceleration of block of mass m2 is 2m/s2. The acceleration of m1 :
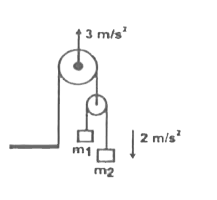 Awill be 8m/s2 upwardBwill be 4m/s2 upwardCwill be 14m/s2 upwardDThe value depends upon actual values of m1 and m2
Awill be 8m/s2 upwardBwill be 4m/s2 upwardCwill be 14m/s2 upwardDThe value depends upon actual values of m1 and m2A particle of mass 'm' moves with a constant speed along a circular path of radius r under the action of a force F .Its speed is given by
A√FrmB√FmrC√FrD√Fmr
Two equal and opposite charges of masses m1 and m2 are accelerated in a uniform electric field through the same distance. What is the ratio of their accelerations, if their ratio of masses is m1m2=0.5?
View SolutionA moving body with a mass m1 strikes a stationary body of mass m2. The masses m1 and m2 should be in the ratio m1m2 so as to decrease the velocity of the first body 1.5 times assuming a perfectly clastic impact. Then the ratio m1m2 is
View SolutionIn the figure shown, all surfaces are smooth and the pulley is massless. A constant force of magnitude F=mg2 is acting on the block of mass M. The acceleration of the block M is :

View SolutionAn object of mass m moves with constant speed in a circular path of radius r under the action of a force of constant magnitude F. the kinetic energy of object is
View SolutionTwo blocks of masses m1 and m2 are connected to each other with the help of a spring. If pushing force F is given to the mass m1 providing acceleration a to it, then acceleration of m2 is
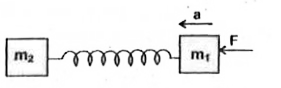
View Solution
