The impulse on a particle due to a force acting on it during a given time interval is equal to the change in its
force
momentum
work done
energy
The correct Answer is:B
To solve the question, we need to understand the relationship between impulse, force, and momentum. Let's break it down step by step.
1. Understanding Impulse:
Impulse (J) is defined as the product of the average force (F) acting on an object and the time interval (Δt) during which the force acts. Mathematically, it can be expressed as:
J=F⋅Δt
2. Newton's Second Law:
According to Newton's second law, the force acting on an object is equal to the rate of change of momentum (p) of that object. This can be expressed as:
F=dpdt
where p is the momentum of the object.
3. Relating Impulse to Momentum:
If we integrate the force over the time interval Δt, we can express the change in momentum as:
J=Δp=pf−pi
where pf is the final momentum and pi is the initial momentum.
4. Conclusion:
Therefore, the impulse on a particle due to a force acting on it during a given time interval is equal to the change in its momentum. Thus, we can conclude:
J=Δp
Final Answer:
The impulse on a particle due to a force acting on it during a given time interval is equal to the change in its momentum.
Impulse (J) is defined as the product of the average force (F) acting on an object and the time interval (Δt) during which the force acts. Mathematically, it can be expressed as:
J=F⋅Δt
According to Newton's second law, the force acting on an object is equal to the rate of change of momentum (p) of that object. This can be expressed as:
F=dpdt
where p is the momentum of the object.
If we integrate the force over the time interval Δt, we can express the change in momentum as:
J=Δp=pf−pi
where pf is the final momentum and pi is the initial momentum.
Therefore, the impulse on a particle due to a force acting on it during a given time interval is equal to the change in its momentum. Thus, we can conclude:
J=Δp
The impulse on a particle due to a force acting on it during a given time interval is equal to the change in its momentum.
Topper's Solved these Questions
Similar Questions
If a particle covers equal distance in equal time intervals, it is said to be in.
View SolutionStatement - 1: A particle moves along a straight line with constant velocity. Now a constant non-zero force is applied on the particle in direction opposite to its initial velocity. After the force is applied, the net work done by this force may be zero in certain time intervals. Statement - 2 : The work done by a force acting on a particle is zero in any time interval if the force is always perpendicular to velocity of the particle.
View Solution
Knowledge Check
A large force is acting on a body for a short time. The impulse imparted is equal to the change in
AaccelerationBmomentumCenergyDvelocityA large force is acting on a body for a short time. The impulse imparted is equal to the change in
AaccelerationBmomentumCenergyDvelocityVelocity-time graph of a particle moving in a straight line is shown in the figure. Mass of the particle is 2 kg. Work done by all the forces acting on the particle in time interval t = 0 to t = 10 sec is
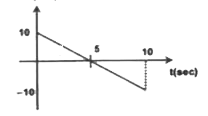 A300JB−300JCzeroD−400J
A300JB−300JCzeroD−400J
The velocity-time graph of a particle moving in a straight line is shown in figure. The mass of the particle is 2kg. Work done by all the forces acting on the particle in time interval between t=0 to t=10s is

View SolutionSTATEMENT-1: Work done by the net force acting on a particle is equal to the change in its kinetic energy.
STATEMENT-2: Change in potential energy is always equal to the work done by external forces.
STATEMENT-3: Work energy theorem is not applicable, if the work is done by the non-conservative forces
View SolutionAssertion: The average velocity of a particle is zero in a time interval. It is possible that the instantaneous acceleration is never zero in the interval.
Reason: The magnitude of average velocity in an interval is equal to its average speed in that interval.
View SolutionThe product of force and the time for which the force acts on a body is equal to the change in ______ of the body.
View SolutionThe displacement of a particle of mass 2kg moving in a straight line varies with times as x=(2t3+2)m. Impulse of the force acting on the particle over a time interval between t = 0 and t = 1 s is
View Solution
