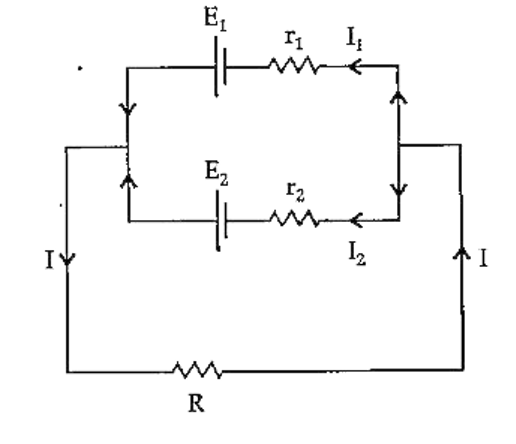
(a) Two cells of emfe and € have their internal resistances $ε_{1} and ε_{2}$ respectively. Deduce an expression for the equivalent emf and internal resistance of their parallel combination when connected across an external resistance R. Assume that the two cells are supporting each other.
(b) In case the two cells are identical, each of emf e= 5V and internal resistance $r = 2 Ω,$ calculate the voltage across the external resistance $R = 10 Ω .$

Text Solution

Verified by Experts

(a). Consider a parallel combination of two cells. Let $ε_{1} and ε_{2}$ be the emfs of two cells and $r_{1} and r_{2}$ their respective internal resistances. $I_{1} and I_{2}$ are the currents leaving the positive electrodes of two cells and at Junction $B_{1}$ , these currents are added up so that net current
$l = l_{1} + l_{2}$ ..........(i)
Let $V (B_{1}) and V (B_{2})$ be the potentials at $B_{1} and B_{2},$ respectively, then considering first cell, we have
$V = V (B_{1}) - V (B_{2}) = ε_{1} - l_{1} r_{1} \Rightarrow l_{1} = \frac{ε_{1} - V}{r_{1}}$ ............(ii)

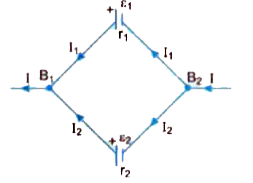
and considering second cell, we have
$V = V (B_{1}) - V (B_{2}) = ε_{2} - l_{1} r_{2} \Rightarrow l_{2} = \frac{ε_{2} - V}{r_{2}} ... ... ... . (i i i)$
$l = l_{1} + l_{2} = \frac{ε_{1} - V}{r_{1}} + \frac{ε_{2} - V}{r_{2}} = (\frac{ε_{1}}{r_{1}} + \frac{ε_{2}}{r_{2}}) - V (\frac{1}{r_{1}} + \frac{1}{r_{2}})$
$\Rightarrow V = [(\frac{ε_{1}}{r_{1}} + \frac{ε_{2}}{r_{2}}) - I] / (\frac{1}{r_{1}} + \frac{1}{r_{2}}) = (\frac{ε_{1} r_{2} + ε_{2} r_{1}}{r_{1} + r_{2}} - I \frac{r_{1} r_{2}}{r_{1} + r_{2}}$ .......(iv)
If instead of two cells we join a single cell having equivalent emf $e_{e q}$ and equivalent internal resistance $e_{e q}$ then we have
$V = ε_{e q} - I r_{e q}$ .........(v)
Thus, comparing (iv) and (v), we get
$e_{e q} = \frac{ε_{1} r_{2} + ε_{2} r_{1}}{r_{1} + r_{2}} and r_{e q} = \frac{r_{1} r_{2}}{r_{1} + r_{2}}$
Alternately, we can write
$\frac{1}{r_{e q}} = \frac{1}{r_{1}} + \frac{1}{r_{2}} and \frac{ε_{e q}}{r_{e q}} = \frac{ε_{1}}{r_{1}} + \frac{ε_{2}}{r_{2}}$
(b) As per question emf of cells $ε_{1} = ε_{2} = 5 V$ , internal resistance of cells $r_{1} = r_{2} = 2 Ω$ and external resistance R=10 V.
Effective emf of cell combination $ε = \frac{ε_{1} r_{2} + ε_{2} r_{1}}{r_{1} + r_{2}} = \frac{5 \times 2 + 5 \times 2}{2 + 2} = 5 V$
and effective internal resistance $r = \frac{r_{1} r_{2}}{r_{1} + r_{2}} = \frac{2 \times 2}{2 + 2} = 1 Ω$
Current in the circuit $I = \frac{ε}{R + r} = \frac{5}{10 + 1} = \frac{5}{11} A$
Voltage across external resistance, $V = I R = \frac{5}{11} \times 10 = 4.55 V$

Updated on:21/07/2023