Two cells of emfs 1.5 V and 2.0v having internal resistance 0.2Σ and 0.3 Σ respectively are connected in parallel . Calculate the emf and internal resistance of the equivalent cell .
To solve the problem of finding the equivalent EMF and internal resistance of two cells connected in parallel, we will follow these steps:
Step 1: Identify the given values
- EMF of cell 1 (E1) = 1.5 V
- Internal resistance of cell 1 (R1) = 0.2 Ω
- EMF of cell 2 (E2) = 2.0 V
- Internal resistance of cell 2 (R2) = 0.3 Ω
Step 2: Calculate the equivalent internal resistance (R_eq)
For resistors in parallel, the formula for the equivalent resistance (R_eq) is given by:
1Req=1R1+1R2
Substituting the values:
1Req=10.2+10.3
Calculating each term:
10.2=5and10.3≈3.33
Now, adding these:
1Req=5+3.33=8.33
Now, taking the reciprocal to find R_eq:
Req=18.33≈0.12Ω
Step 3: Calculate the equivalent EMF (E_eq)
The equivalent EMF for cells in parallel can be calculated using the formula:
Eeq=E1/R1+E2/R21/R1+1/R2
Substituting the values:
Eeq=(1.5/0.2)+(2.0/0.3)(1/0.2)+(1/0.3)
Calculating the numerator:
1.50.2=7.5and2.00.3≈6.67
So,
Numerator=7.5+6.67=14.17
Calculating the denominator (which we already found):
Denominator=8.33
Now, substituting back into the equation for E_eq:
Eeq=14.178.33≈1.70V
Final Results
- Equivalent EMF (E_eq) = 1.70 V
- Equivalent Internal Resistance (R_eq) = 0.12 Ω
Summary
Thus, the equivalent cell has an EMF of approximately 1.70 V and an internal resistance of approximately 0.12 Ω.
---
- EMF of cell 1 (E1) = 1.5 V
- Internal resistance of cell 1 (R1) = 0.2 Ω
- EMF of cell 2 (E2) = 2.0 V
- Internal resistance of cell 2 (R2) = 0.3 Ω
For resistors in parallel, the formula for the equivalent resistance (R_eq) is given by:
The equivalent EMF for cells in parallel can be calculated using the formula:
- Equivalent EMF (E_eq) = 1.70 V
- Equivalent Internal Resistance (R_eq) = 0.12 Ω
Thus, the equivalent cell has an EMF of approximately 1.70 V and an internal resistance of approximately 0.12 Ω.
Topper's Solved these Questions
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - Section -C7videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - Section-E17videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - Section -A14videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
Two cells of 1.5 V and 2 V , having internal resistances of 1Ω and 2Ω respectively, are connected in parallel so as to read the current in the same direction through an external resistance of 5Ω . The current in the external resistance will be
View SolutionIf three cell are connected in parallel then equivalent emf……. and equivalent internal resistance is …..
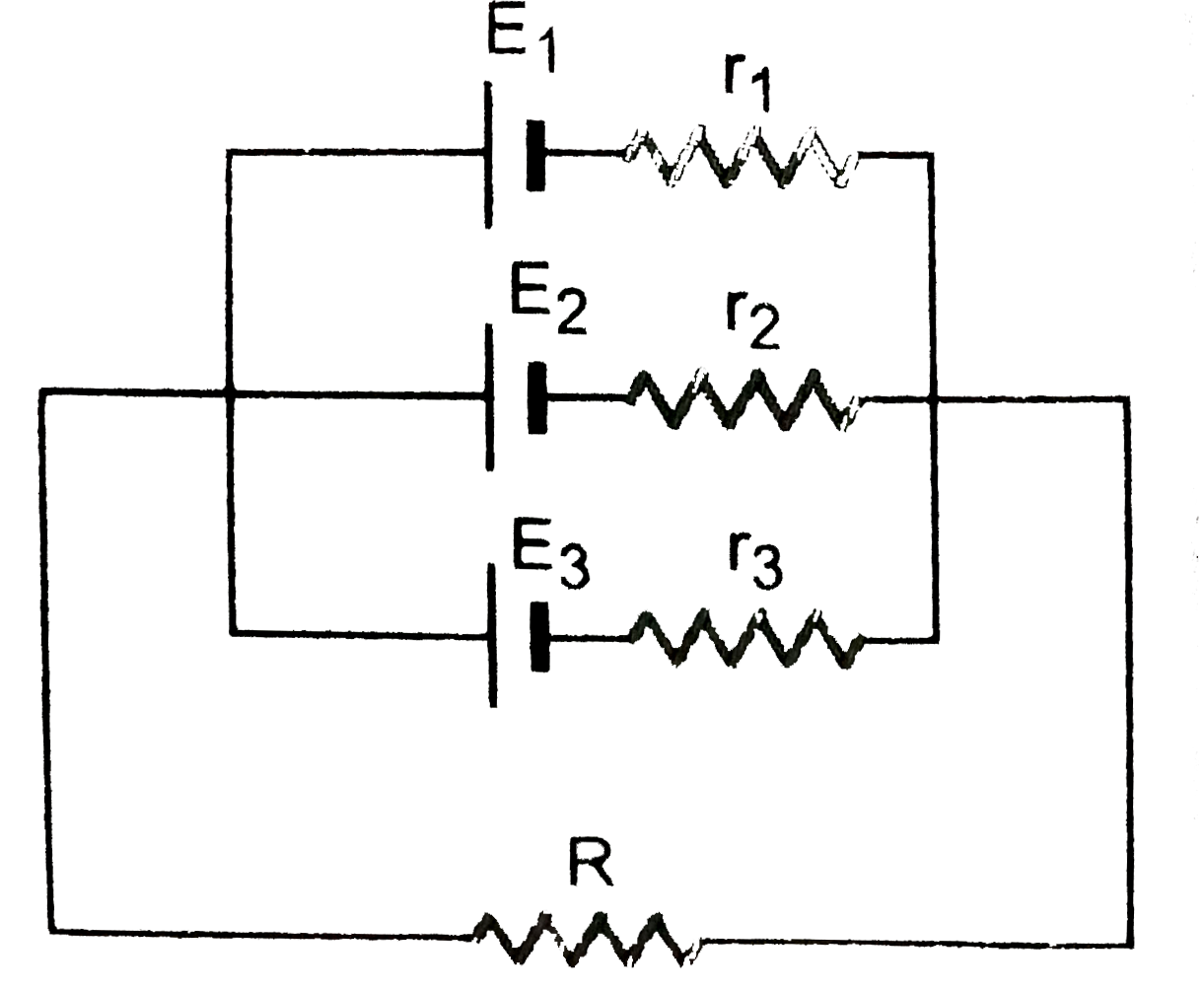 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If n cells each of emf E and internal resistance rare connected in parallel, then the total emf and internal resistances will be
Aε,rnBε,nrCnε,rnDnε,nr
Two cells of emfs ε1andε2 and internal resistances r1andr2 respectively are connected in parallel . Obtain expressions for the equivalent (i) resistance and , (ii) emf of the combination.
View SolutionFive cells each of emf E and internal resistance r are connecte in series. Due to oversight one cell is connected wrongly . The equivalent emf and internal resistance of the combination is
View SolutionIn the circuit shown in fig. the cell has emf 10V and internal resistance 1Ω
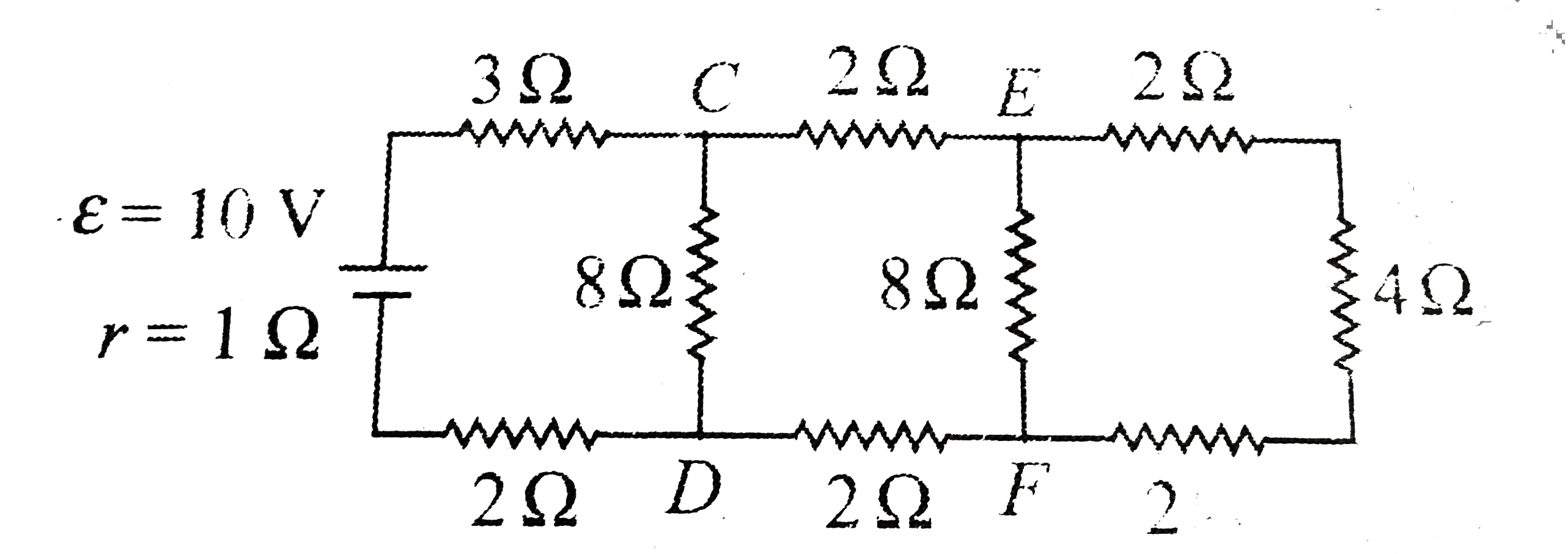 View Solution
View SolutionTwo cells having an internal resistance of 0.2Ω and 0.4Ω are connected in parallel (same polarity) the voltage across the battery is 1.5 V. If the emf of one cell is 1.2 V, then the emf of second cell is
View SolutionTwo cells of emf E1 and E2 have internal resistance r1 and r2. Deduce an expression for equivalent emf of their parallel combination.
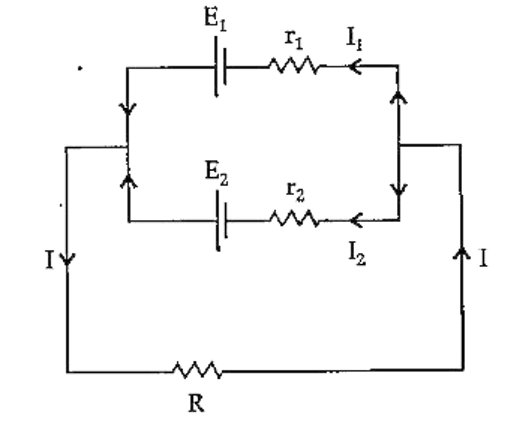 View Solution
View Solution24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View SolutionMaximum current produced by a cell of emf 10 V and internal resistance 2Ω is
View Solution

