(a) Write an expression of magnetic moment associated with a current (l) carrying circular coil of radius R having N turns.
(b) Consider the above mentioned coil placed in YZ plane with its centre at the origin. Derive expression for the value of magnetic field due to it at point (x, 0, 0).

Text Solution

Verified by Experts

(a) Magnetic moment of a coil carrying current is given as m= NIA, where A is the area bounded by the loop, If R be radius of coil then $A = π R^{2}$ and so magnetic moment $M = N I . π R^{2}$ .
(b) Let the said coil be placed in Y- Z plane with its centre at the origin and let P be a point along x-axis at a distance from origin [i.e, having coordinates (x, 0, 0)). A turn of coil may be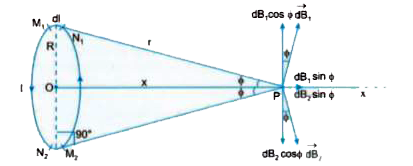
divided into large number of current elements $I . \to d l$ . Two such elements $N_{1} M_{1} and N_{2} M_{2}$ , diametrically opposite to each other, produce the magnetic fields $d {\to B}_{1} and d {\to B}_{2}$ perpendicular to both $\to r and \to d l$ and given by right hand rule as,
$∣ ∣ \to d B_{1} ∣ ∣ = ∣ ∣ d {\to B}_{2} ∣ ∣ = \frac{μ_{0}}{4 π} \frac{I d l {sin 90}^{\circ}}{4 π} . \frac{I d l {sin 90}^{\circ}}{r^{2}} = \frac{μ_{0}}{4 π} \frac{I d l}{(R^{2} + x^{2})}$
These fields may be resolved into components along x-axis and y-axis. Obviously components along y-axis balance each other but components along x-axis are all summed up. Hence, magnetic field due to whole current loop will be :
$B = \oint d B sin ϕ = \oint \frac{μ_{0}}{4 π} \frac{I d l}{(R^{2} + x^{2}) . \frac{R}{\sqrt{(R^{2} + x^{2})}} = \frac{μ_{0} I R}{4 π {(R^{2} + x^{2})}^{3 / 2}} \oint d l}$
$= \frac{μ_{0} I R}{4 π {(R^{2} + x^{2})}^{3 / 2}} .2 π R = \frac{μ_{0} I R^{2}}{2 {(R^{2} + x^{2})}^{3 / 2}}$
As the coil consists of N turns, all carrying same current 1 in same direction so their magnetic up and the field due to entire coil will be.
$B = \frac{μ_{0} N I R^{2}}{2 {(R^{2} + x^{2})}^{3 / 2}}$

Updated on:21/07/2023