(a) Derive the expression for the torque acting on the rectangular current carrying coll of a galvanometer. Why is the magnetic field made radial ?
(b) A α- particle is accelerated through a potential difference of 10 kV and moves along y-axis. It enters in a region of uniform magnetic field B=2×10−3T acting along y-axis. Find the radius of its path. [Take mass of α−particle =6.4×10−27kg]
(a) Consider a rectangular galvanometer coil PQRS of length land breadth b, carrying a current l, placed in a uniform magnetic field B such that a vector normal to the plane of the coil subtends an angle θ from the direction of dB.
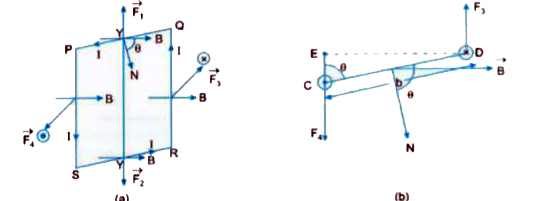
In this situation forces F and E, having magnitude Ib B sin θ are acting on arms PQ and RS. The forces are equal, opposite and collinear, hence they cancel out.
Again forces F3andF4 having magnitude ll B are acting on each of the two arms QR and SP. These forces too are equal and opposite but these are non-collinear and form a couple. Figure (b) represents a top view of the arrangement and from it, we find that the torque of the couple acting on the loop.
τ=(IIB)×bsinθ=l(lb)Bsinθ=IABsinθ
where A =l b= area of the loop. If anstead of a single loop, we have a rectangular coil having N turns, then
torque τ=NIABsinθ
In vector notation →τ=NI(→A×→B)=(→m×→B), where →m=NI→A= magnetic moment of current carrying coil.
The magnetic field is made radial so that value of θ becomes 90∘ and in that case torque τ=NIAB, whose value does not change even when the coil rotates by a certain angle.
(b) Here accelerating voltage V=10kV=10×103V, normal magnetic field B=2×10−3T mass of α -particles m=6.4×10−27kg and charge of α-particle q=+2e=2×1.6×10−19=3.2x10−19C
Radius of circular path r=√2mVqB2=
⎷2×(6.4×10−27)×10×103(3.2×10−19)×(2×10−3)2=10m
Similar Questions
(a) Derive the expression for the torque acting on a current carrying placed in a magnetic field.
(b) Explain the significance of a radial magnetic when current carrying coil is kept in it.
View SolutionObtain the expression for the deflecting torque acting on the current carrying rectangular coil of a galvanometer in a uniform magnetic field. Why is a radial magnetic field employed in the moving coil galvanometer?
View Solution
Knowledge Check
A proton and an α particle accelerated through the same potential difference enter a region of uniform magnetic field normally if the radius of the proton orbit is 10 cm ten radius of α particle is
A10cmB10√2cmC20cmD5√2cm
A proton and α - particle are accelerated with same potential difference and they enter in the region of constant magnetic field B perpendicular to the velocity of particles. Find the ratio of radius of curvature of α - particle.
View SolutionA proton and α−partic≤ are accelerated with same potential difference and they enter in the region of constant magnetic field B perpendicular to the velocity of particles. Find the ratio of radius of curvature of alpa−partic≤.
View SolutionA charged particle is accelerated through a potential difference of 24kV and acquires a speed of 2×106m/s.It is then injected perpendicularly into a magnetic field of strength 0.2T.Find the radius of the circle described by it.
View SolutionA charged particle of mass m and charge q is accelerated through a potential difference of V volts. It enters a region of uniform magnetic field which is directed perpendicular to the direction of motion of the particle. Find the radius of circular path moved by the particle in magnetic field.
View SolutionA charged particle of mass m and charge q is accelerated through a potential difference of V volts. It enters a region of uniform magnetic field which is directed perpendicular to the direction of motion of the particle. Find the radius of circular path moved by the particle in magnetic field.
View SolutionA proton and an α-particle, accelerated through same potential difference, enter a region of uniform magnetic field with their velocities perpendicular to the field. Compare the radii of circular paths followed by them.
View SolutionA proton and an α-particle, accelerated through same potential difference, enter a region of uniform magnetic field with their velocities perpendicular to the field. Compare the radii of circular paths followed by them.
View Solution
