Figure shows the stopping potential $(V_{0})$ for the photo electron vers $(\frac{1}{λ})$ graph, for two metals A and B, $λ$ being the wavelength of incident light.

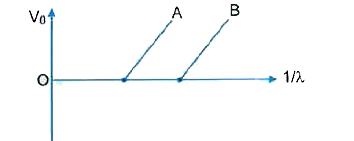
How is the value of Planck's constant determined from the graph ?

Text Solution

Verified by Experts

We know that $V_{0} = \frac{h}{e} (v - v_{0}) = \frac{h c}{e} (\frac{1}{λ} - \frac{1}{λ_{0}})$ .
So $V_{0} - \frac{1}{λ}$ graph is a straight line graph whose slope has a magnitude of $\frac{h c}{e}$ .
Thus, Planck.s constant $h = \frac{e}{c} \times (Slope of V_{0} - \frac{1}{λ}$ aph for any photosensitive metal)

|

Updated on:21/07/2023

Class 12 PHYSICS CBSE EXAMINATION PAPER 2020 (SOLVED)

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The stopping potential are $V_{1}$ and $V_{2}$ . Calculate the $(V_{1} - V_{2})$ , if the $λ_{1}$ and $λ_{2}$ are wavelength of incident lights, respectively.
A $\frac{h c}{e} (\frac{1}{λ_{1}} - \frac{1}{λ_{2}})$
B $\frac{h c}{e} (\frac{1}{λ_{1}} + \frac{1}{λ_{1}})$
C $\frac{e}{h c} (\frac{1}{λ_{1}} + \frac{1}{λ_{2}})$
D $\frac{e}{h c} (\frac{1}{λ_{1}} - \frac{1}{λ_{2}})$
Question 2 - Select One
If $λ_{0}$ is the threshold wavelnegth of a metal and $λ$ is the wavelength of the incident radiation, the maximum velocity of the ejected electron from the metal would be
A ${[\frac{2 h c}{m} (\frac{λ_{0} - λ}{λ_{0} λ})]}^{1 / 2}$
B ${[\frac{2 h c}{m} (\frac{λ - λ_{0}}{λ λ_{0}})]}^{1 / 2}$
C ${[\frac{2 h c}{m} (λ - λ_{0})]}^{1 / 2}$
D ${[\frac{2 h c}{m} (λ_{0} - λ)]}^{1 / 2}$
Question 3 - Select One
In photo electric effect, the slope of the straight line graph between stopping potential and frequency of the incident light gives the ratio of Planck's constant to
Acharge of electron
Bwork function
Cphoto electric current
D $K . E .$ of electron

U-LIKE SERIES-CBSE EXAMINATION PAPER 2020 (SOLVED)-SECTION B

Home
Ask Doubt
Profile