Draw a graph showing the variation of stopping potential with frequency of the incident on a metal plate. How can the value of Planck's constant be determined from this graph?
To solve the problem of drawing a graph showing the variation of stopping potential (V₀) with the frequency (ν) of incident radiation on a metal plate, and determining the value of Planck's constant (h) from this graph, we can follow these steps:
1. Understand the Photoelectric Effect:
The photoelectric effect describes how electrons are emitted from a metal surface when it is exposed to light of sufficient frequency. The energy of the incident photons must be greater than the work function (φ₀) of the metal for electrons to be emitted.
2. Use Einstein's Photoelectric Equation:
The relationship between stopping potential (V₀), frequency (ν), Planck's constant (h), and the work function (φ₀) is given by:
eV₀=hν−φ₀
where e is the charge of an electron.
3. Rearrange the Equation:
Rearranging the equation to express V₀ in terms of ν:
V₀=heν−φ₀e
This equation is in the form of a straight line y=mx+c, where:
- y is V₀ (stopping potential),
- x is ν (frequency),
- m=he (slope of the line),
- c=−φ₀e (y-intercept).
4. Draw the Graph:
- On the x-axis, plot the frequency (ν).
- On the y-axis, plot the stopping potential (V₀).
- The graph will be a straight line starting from the y-intercept at −φ₀e and will have a positive slope.
5. Identify the Threshold Frequency:
The line will not extend below the threshold frequency (ν₀), which corresponds to the minimum frequency required to emit electrons. Below this frequency, no photoelectrons are emitted, and thus V₀ will be zero.
6. Determine Planck's Constant (h):
From the slope (m) of the line:
m=he
Rearranging gives:
h=m⋅e
To find h, measure the slope of the line and multiply it by the charge of an electron (approximately 1.6×10−19C).
Graph Representation:
- The graph will show a straight line starting from the y-intercept at −φ₀e and rising with a slope of he.
- The x-axis (frequency) will have a threshold frequency (ν₀) where the line begins.
The photoelectric effect describes how electrons are emitted from a metal surface when it is exposed to light of sufficient frequency. The energy of the incident photons must be greater than the work function (φ₀) of the metal for electrons to be emitted.
The relationship between stopping potential (V₀), frequency (ν), Planck's constant (h), and the work function (φ₀) is given by:
eV₀=hν−φ₀
where e is the charge of an electron.
Rearranging the equation to express V₀ in terms of ν:
V₀=heν−φ₀e
This equation is in the form of a straight line y=mx+c, where:
- y is V₀ (stopping potential),
- x is ν (frequency),
- m=he (slope of the line),
- c=−φ₀e (y-intercept).
- On the x-axis, plot the frequency (ν).
- On the y-axis, plot the stopping potential (V₀).
- The graph will be a straight line starting from the y-intercept at −φ₀e and will have a positive slope.
The line will not extend below the threshold frequency (ν₀), which corresponds to the minimum frequency required to emit electrons. Below this frequency, no photoelectrons are emitted, and thus V₀ will be zero.
From the slope (m) of the line:
m=he
Rearranging gives:
h=m⋅e
To find h, measure the slope of the line and multiply it by the charge of an electron (approximately 1.6×10−19C).
- The graph will show a straight line starting from the y-intercept at −φ₀e and rising with a slope of he.
- The x-axis (frequency) will have a threshold frequency (ν₀) where the line begins.
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - NCERT Exerciese question
1 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Short answer
1 Videos
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Problems for Practice (B)
2 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Multiple Choice Questions
1 Videos
Similar Questions
Draw and explain the graph showing the variation of stopping potential with frequency of incident radiation in relation to photoelectric effect.
View SolutionDraw a graph showing the variation of stopping potential with frequency of the incident radiation. What does the slope of the line with frequency axis indicate? What information can be obtained from the values of intercept on the potential axis?
View Solution
Knowledge Check
In a photocell circuit the stopping potential, V0, is a measure of the maximum kinetic energy of the photoelectrons. The following graph shows experimentally measured values of stopping potential versus frequency v of incident light.
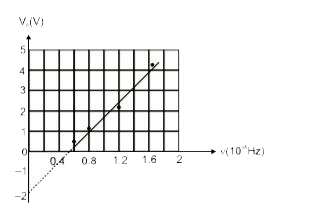
The values of Planks constant and the work function as determined from the graph are (taking the magnitude of electronic charge to be e=1.6×10−19C)A6.4×10−34Js,2.0eVB6.0×10−34Js,2.0eVC6.4×10−34Js,3.2eVD6.0×10−34Js,3.2eV
Draw a graph showing the variation of decay rate with number of active nuclei.
View SolutionDraw a graph showing the variation of decay rate with number of active nuclei.
View SolutionDefine photoelectric effect. Draw a graph to show the variation of stopping potential with frequency of incident radiation on a metal plate.
View SolutionSketch a graph showing the variation of reactance of an inductor with frequency of the applied voltage
View SolutionSketch the graphs, showing the variation of stopping potential Vs with frequency v of the incident radiations for two photosensitive materials A and B having threshold frequencies v0>v'0 respectively.
(i) which of the two metals A or B has higher work function?
(ii) What information do you get from the slope of the graphs?
(iii) What does the value of the intercept of graph A on the potential axis represent?
View SolutionPlot a graph showing variation of stopping potential (V0) with the frequency (v) of the incident radiation for a given photosensitive material. Hence, state the significance of the threshold frequency in photoelectric emission.
Using the principle of energy conservation, write the equation relating the energy of incident photon, threshold frequency and the maximum kinetic energy of the emitted photoelectrons.
View SolutionDraw a graph showing variation of de-Broglie wavelength with the momentum of an electron.
View Solution
