A line y=mx+1 intersects the circle (x−3)2+(y+2)2=25 at the points P and Q . If the midpoint of the line segment PQ has x-coordinate −35, then which one of the following options is correct ?
6≤m<8
−3≤m<−1
4≤m<6
2≤m<4
The correct Answer is:D
(Key idea : Firstly find the centre of the given circle and write the coordinate of mid point (A),of line sequment PQ, since Ac⊥PQ therefore use (slope of AC)x(slope of PQ)=−1.
It is given that points P and Q are intersecting points of circle.
(x−3)2+(y+2)2=25 .....(i)
Line y=mx+1 .....(ii)
And , the mid -point of PQ is A having x-coordinate −35 so y-coordinate is 1−35m.
So, A(−35,1−35M)
From the figure,
∵AC⊥PQ
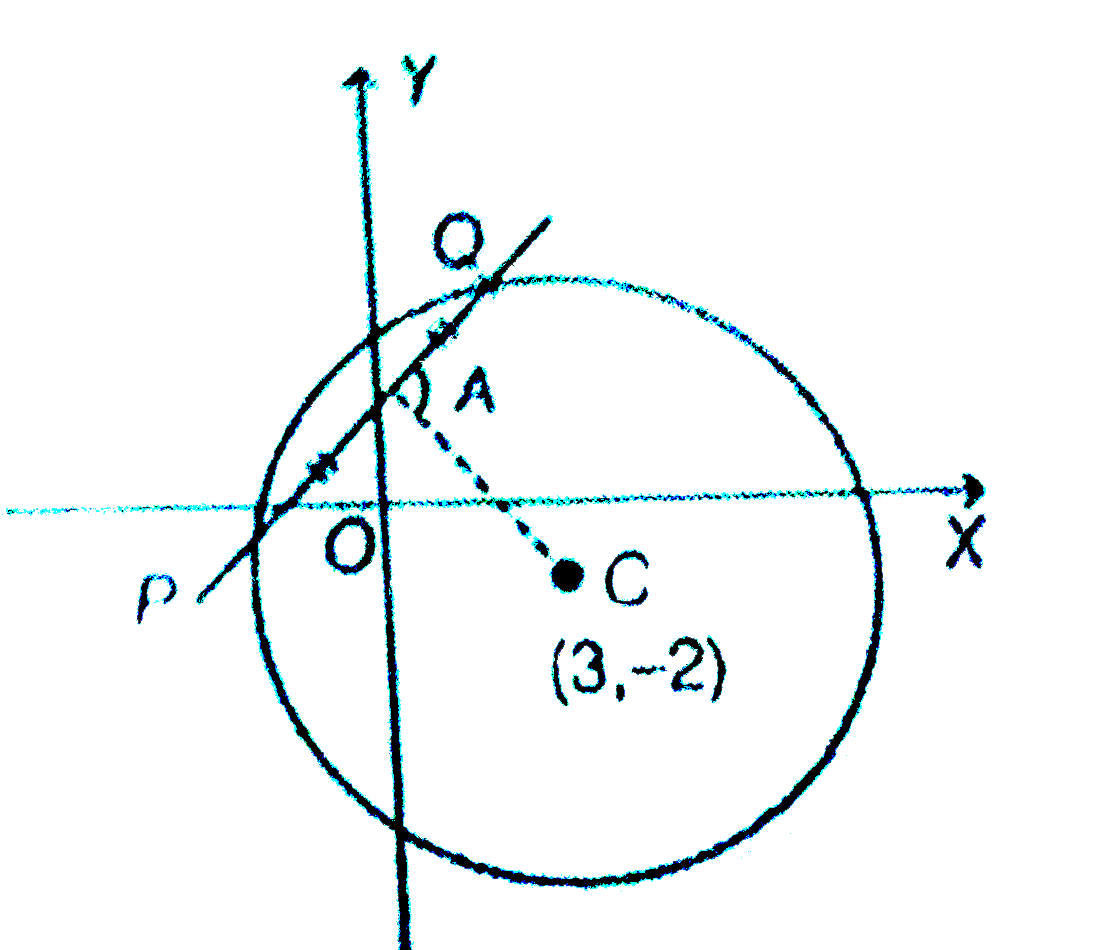
⇒ (slope of AC)x (slope of PQ)=−1.
⇒⎛⎝−2−1+35m3+35⎞⎠×m=−I
⇒3m2−15m+18=0
⇒m=2or3.
Topper's Solved these Questions
- SOLVED PAPER 2019BOOK - IIT JEE PREVIOUS YEARCHAPTER - SOLVED PAPER 2019EXERCISE - Paper -1 section-2
8 Videos
- SOLVED PAPER 2019BOOK - IIT JEE PREVIOUS YEARCHAPTER - SOLVED PAPER 2019EXERCISE - Paper -1 section-3
6 Videos
- SEQUENCES AND SERIESBOOK - IIT JEE PREVIOUS YEARCHAPTER - SEQUENCES AND SERIESEXERCISE - RELATION BETWEEN AM,GM, HM AND SOME SPECIAL SERIES
34 Videos
- STRAIGHT LINE AND PAIR OF STRAIGHT LINESBOOK - IIT JEE PREVIOUS YEARCHAPTER - STRAIGHT LINE AND PAIR OF STRAIGHT LINESEXERCISE - GENERAL EQUATION OF PAIR OF STRAIGHT LINES (Objective Questions I) (Only one correct option)
1 Videos
Similar Questions
Knowledge Check
A line y=mx+1 meets the circle (x−3)2+(y+2)2=25 at point P and Q. if mid point of PQ has abscissa of −35 then value of m satisfies
A6≤m<8B2≤m<4C−3≤m<−1D4≤m<6The line x=2y intersects the ellipse x24+y2=1 at the points P and Q. The equation of the circle with PQ as diameter is
Ax2+y2=12Bx2+y2=1Cx2+y2=2Dx2+y2=52The line y=mx+c intersects the circle x2+y2=a2 in two distinct real points if
A−a√a+m2<cBc<a√1+m2C−c√1+m2<aDa<c√1+m2
A line intersects the y-axis and x-axis at the points P and Q respectively. If (2, 5) is the mid-point of PQ, then find the coordinates of P and Q.
View SolutionA line intersects the y-axis and x-axis at the points P and Q respectively. If (2,-5) is the mid-point of PQ then find the coordinates of P and Q.
View SolutionA line intersects the y-axis and x-axis at the points P and Q respectively. If (2, 5) is the mid-point of PQ, then find the coordinates of P and Q.
View SolutionA line intersect the Y-axis and X-axis at he points P and Q respectively. If (2,-5) is the mid-point of PQ, then find the coordinate of P and Q.
View SolutionThe straight line x−2y+5=0 intersects the circle x2+y2=25 in points P and Q, the coordinates of the point of the intersection of tangents drawn at P and Q to the circle is
View Solution
