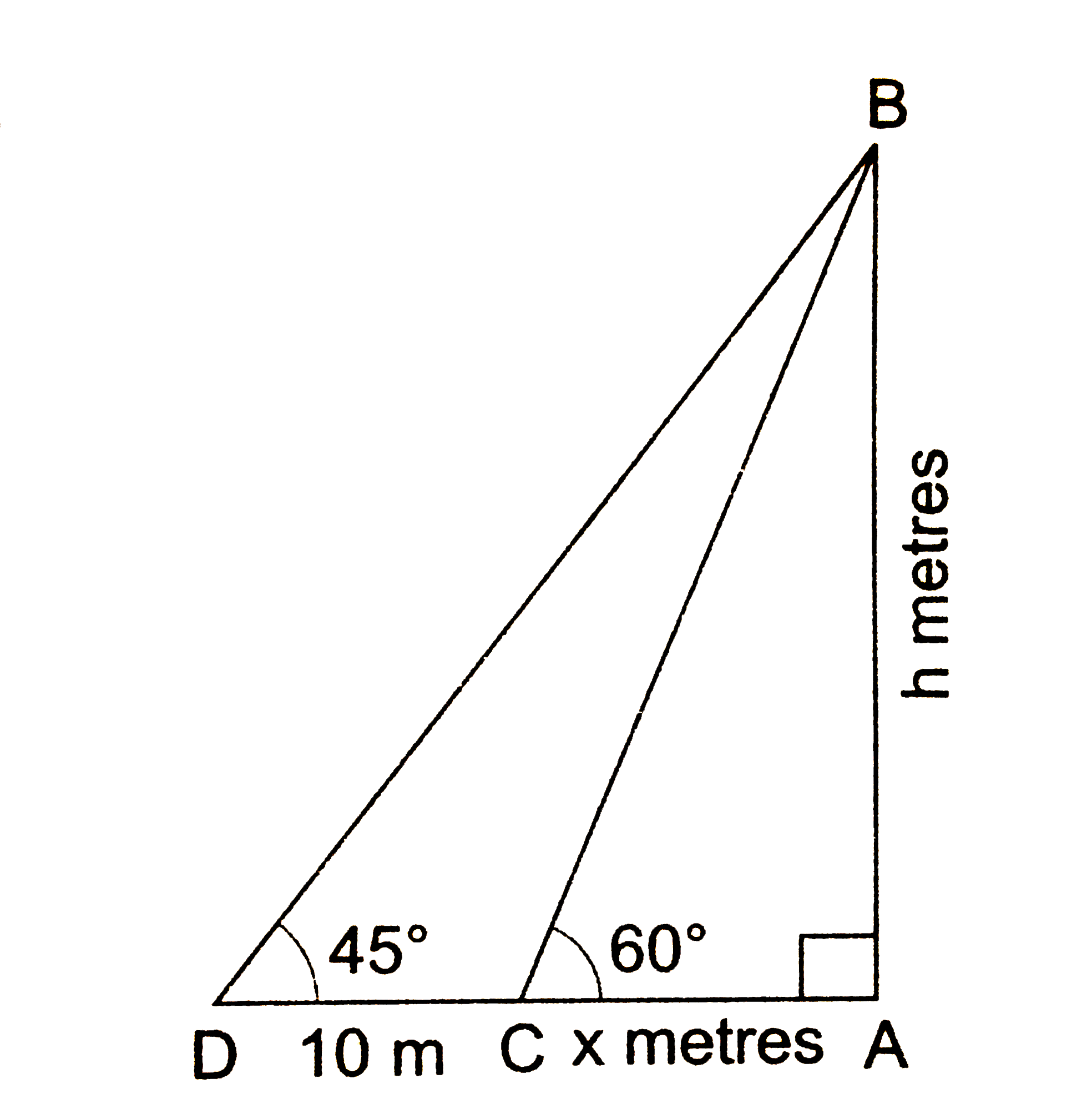
The shadow of a tower, when the angle of elevation of the summit is 45∘, is found to be 10metres longer than when the angle of elevation, when 60∘. Find the height of the tower.
21.67
23.66
22.68
23.88
The correct Answer is:B
Let AB be the tower and the let AC and AD be its shadows when the angle of elevation of the sum are 60∘ and 45∘ respectively.
∴∠ACB=60∘,∠ADB=45∘,
∠DAB=90∘ and ∠CD=10m.
Let AB=h metres and AC=x metres.
From right ΔCAB, we get
ACAB=cot602=1√3.
⇒xh=1√3⇒x=−h√3............(i).
From right ΔDAB, we get
ADAB=cot45∘=1⇒x+10h=1
⇒x+10=h⇒x=h−10..............
Equating the values of x from (i) and (ii), we get
h√3=h−10⇒h=√3h−10√3⇒(√3−1)h=10√3
⇒h=10√3(√3−1)=⎧⎪
⎪⎨⎪
⎪⎩10√3(√3−1)×(√3+1)(√3+1)⎫⎪
⎪⎬⎪
⎪⎭
=5√3(√3+1)=15+5√3.
⇒h=(5+5×1.732)=(15+8.66)=23.66.
Topper's Solved these Questions
- HEIGHTS AND DISTANCESBOOK - RS AGGARWALCHAPTER - HEIGHTS AND DISTANCESEXERCISE - Exercise 14
38 Videos
- HEIGHTS AND DISTANCESBOOK - RS AGGARWALCHAPTER - HEIGHTS AND DISTANCESEXERCISE - Multiple Choice Questions (Mcq)
25 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
34 Videos
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - QUESTION
2 Videos
Similar Questions
The shadow of a tower,when the angle of elevation of the sum is 45∘ , is found to be 10metres longer than when the angle of elevation, when 60∘. Find the height of the tower.
View SolutionThe shadow of a tower, when the angle of elevation of the sun is 45o , is found to be 10m. longer than when it was 60o . Find the height of the tower.
View Solution
Knowledge Check
On the level ground, the angle of elevation of a tower is 30∘. On moving 20 m nearer, the angle of elevation is 60∘. The height of the tower is
A10 mB20 mC10√3mDNoneThe angle of elevation of the top of a tower at point on the ground is 30∘. If on walking 20 metres towards the tower, the angle of elevation become 60∘ then the height of the tower is
A10 metresB10√3 metresC10√3mDNone of these
The shadow of a tower , when the angle of elevation of the sum is 30∘ is found to be 10 metre longer than when it was 60∘ .The height of the tower will be :
View SolutionThe angle of elevation of a tower at a point is 45∘. After going 40 m towards the foot of the tower, the angle of elevation of the tower becomes 60∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the same level as the foot of tower is ϕ. On moving 'a' mctrcs towards the foot of tower, the angle of elevation becomes 45∘ and again on moving b metres in the same dorection, the angle of elevation becomes (90∘−ϕ). Find the height of the tower.
View SolutionThe shadow of a tower standing on a level plane is found to be 50 m longer when when sun's elevation is 30∘ than when it is 60∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower at a point A on the ground is 30∘. On walking 20 meters toward the tower, the angle of elevation is 60∘. Find the height of the tower and its distance from A.
View SolutionThe angle of elevation of the top of a tower from a point at a distance of 100 metres from its foot on a horizontal plane is found to be 60∘ . Find the height of the tower
View Solution
