Question

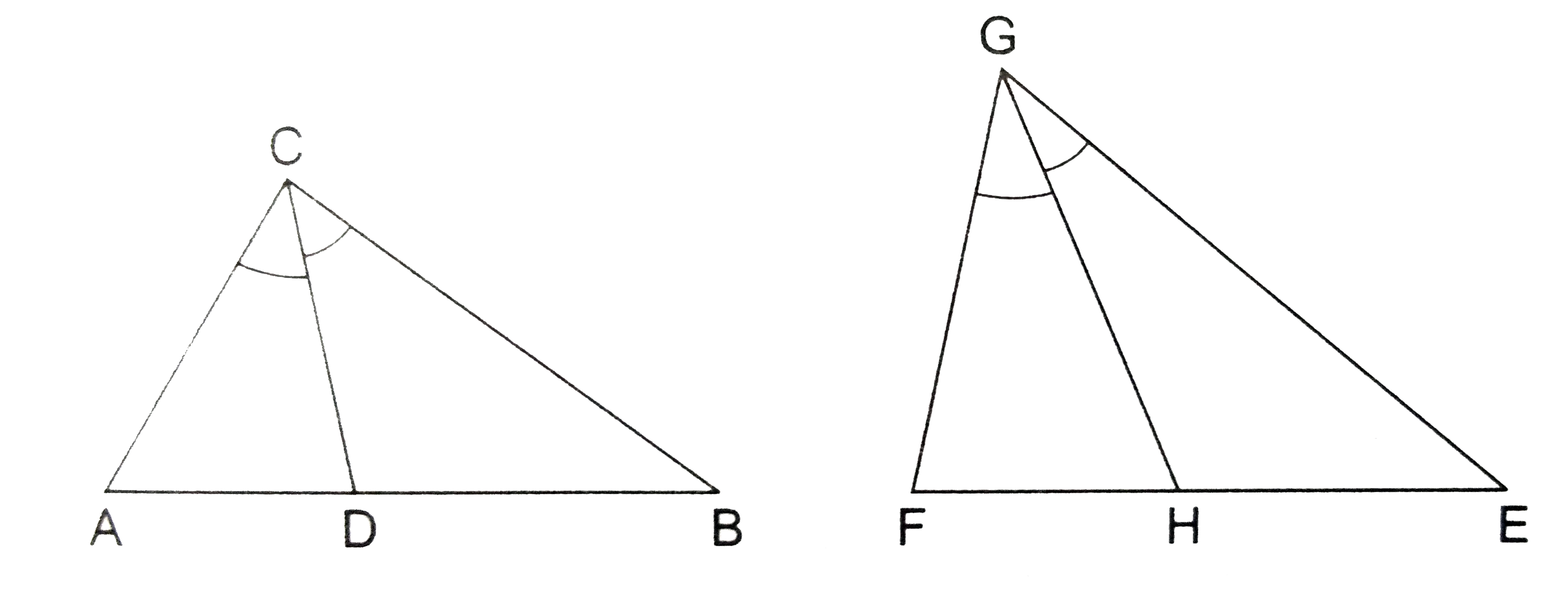
In the given figure, BM and EN are respectively the medians of $\Delta ABC\text{and}\Delta DEF$. If $\Delta ABC~\Delta DEF$, prove that:
(a) $\Delta AMB~\Delta DNE$
$\left(b\right)\Delta CMB~\Delta FNE$
( c) $\frac{BM}{EN}=\frac{AC}{DF}$

Explanation

`Delta ABC~ Delta DEF` (given)
`:. angle A= angle D, angle B= angleE and angle C= angle F " "…(i)`
`and (AB)/(DE)=(BC)/(EF)=(CA)/(FD)" "…(ii)`
Since BM and EN are medians, we have
`CA=2AM=2CM and FD= 2DN= 2FN`
`:.` from (ii), we get
`(AB)/(DE)=(BC)/(EF)=(CA)/(FD)=(2AM)/(FD)=(2AM)/(2DN)=(2CM)/(2FN)`
`rArr (AB)/(DE)=(BC)/(EF)=(CA)/(FD)=(AM)/(DN)=(CM)/(FN) " "....(iii)`
(a) In `Delta AMB = angle EDN[ :. angle A = angle D` from (i)]
`and (AB)/(DE)/(AM)/(DN)` [ from (iii)]
`:. Delta AMB~ Delta DNE` [ by SAS-similarity]
(b) In ` Delta CMB and Detla FNE` , we have
` angle BCM= angleEFN= [ :. angle C= angle F ` from (i) ]
and `(BC)/(EF)=(CM)/(FN)` [ from (iii)]
(c) ASs proved above `Delta AMB ~ Delta DNE` and also so `(AB)/(DE)=(BM)/(EN) " " ...(iv)`
From (ii) and (iv), we get
`(BM)/(EN)=(AC)/(FD)`