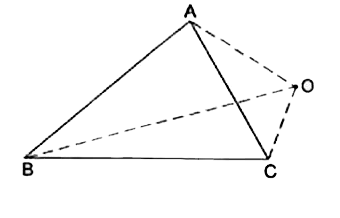
If O is a point within a quadrilateral ABCD, show that
To prove that OA+OB+OC+OD>AC+BD for a point O inside quadrilateral ABCD, we can follow these steps:
Step 1: Consider Triangle AOC
In triangle AOC, by the triangle inequality theorem, the sum of the lengths of any two sides must be greater than the length of the third side. Therefore, we have:
OA+OC>AC(1)
Step 2: Consider Triangle BOD
Similarly, in triangle BOD, applying the triangle inequality theorem gives us:
OB+OD>BD(2)
Step 3: Combine the Inequalities
Now, we can combine the inequalities from Step 1 and Step 2. Adding both inequalities (1) and (2) together, we get:
(OA+OC)+(OB+OD)>AC+BD
This simplifies to:
OA+OB+OC+OD>AC+BD
Conclusion
Thus, we have shown that:
OA+OB+OC+OD>AC+BD
This completes the proof.
In triangle AOC, by the triangle inequality theorem, the sum of the lengths of any two sides must be greater than the length of the third side. Therefore, we have:
OA+OC>AC(1)
Similarly, in triangle BOD, applying the triangle inequality theorem gives us:
OB+OD>BD(2)
Now, we can combine the inequalities from Step 1 and Step 2. Adding both inequalities (1) and (2) together, we get:
(OA+OC)+(OB+OD)>AC+BD
This simplifies to:
OA+OB+OC+OD>AC+BD
Thus, we have shown that:
OA+OB+OC+OD>AC+BD
This completes the proof.
Topper's Solved these Questions
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10B
27 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10C
18 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXAMPLE
32 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
Similar Questions
Knowledge Check
A point O lies inside a square ABCD such that OA=3, OB=4 and OD=5, find the value of OC.
AA)3√3BB)6.67CC)3√2DD)4√2In a quadrilateral ABCD, ¯¯¯¯¯¯AC⊥¯¯¯¯¯¯BD and AB=AD. ABCD is a ________
ATrapeziumBRhombusCRectangleDKiteIn a quadrilateral ABCD, ¯¯¯¯¯¯AC⊥¯¯¯¯¯¯BD and AB=AD. ABCD is a ________
AtrapeziumBrhombusCrectangleDKite
If O is point in the exterior of △ABC,show that 2(OA+OB+OC)>(AB+BC+CA)
View SolutionThe given figure shows a quadrilateral ABCD. Prove that :
AB+BC+CD+DA>AC+BD

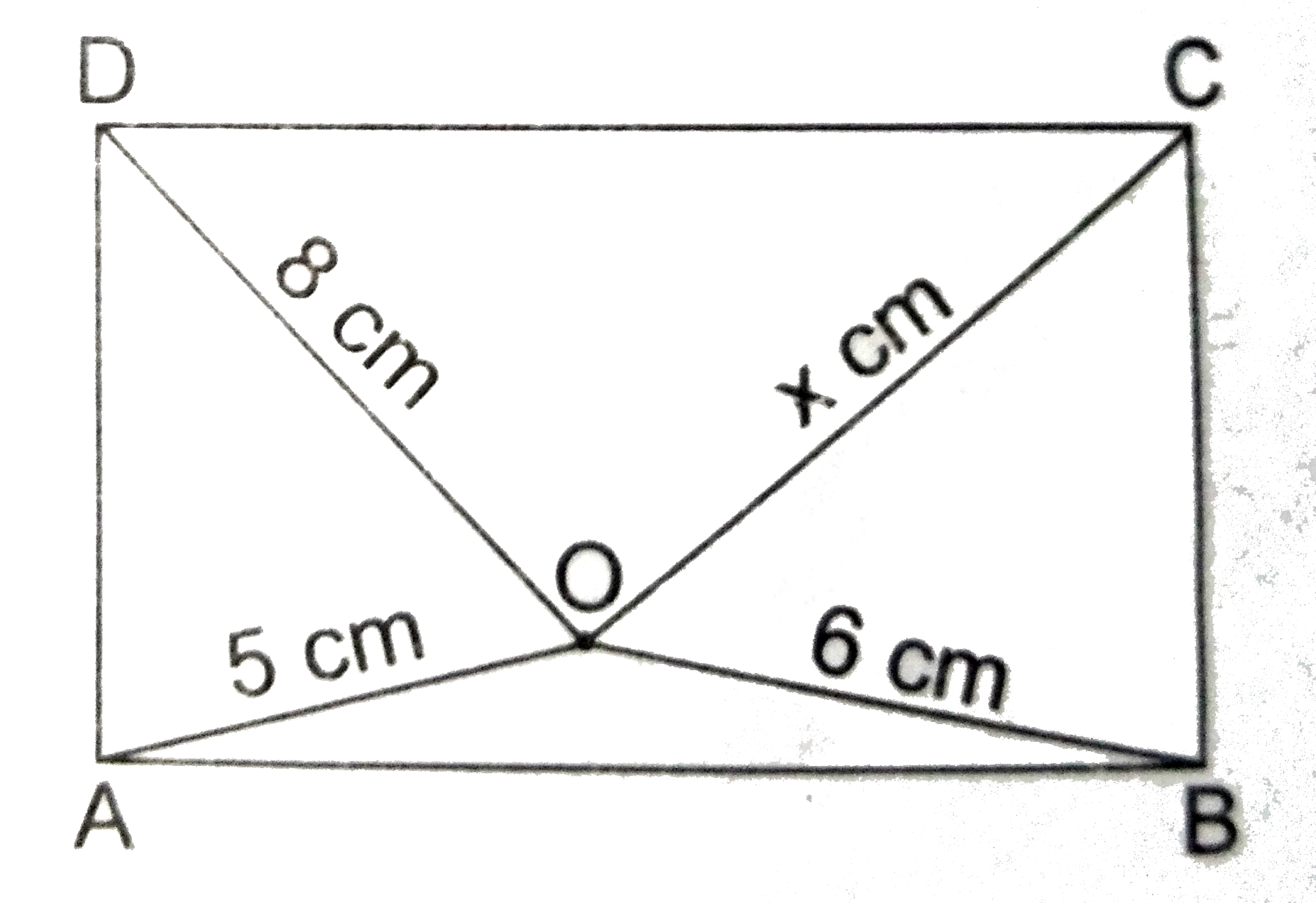
View SolutionO is any point inside a rectangle ABCD. Prove that OB2+OD2=OA2+OC2.
DEDUCTION In the given figure, O is a point inside a rectangle ABCD such that OB=6cm,OD=8cmandOA=5cm, find the length of OC.
View SolutionIn the figure, diagonals AC and BD of quadrilateral ABCD intersect at 0 such that OB = OD. If AB = CD, then show that

DA I I CB or ABCD is a parallelogram.
View SolutionIf AC and BD are the diagonals of a quadrilateral ABCD, prove that its area is equal to 12∣∣∣−−→AC×−−→BD∣∣∣.
View Solution
