Given aΔABC in which ∠B=90∘andAB=√3BC. Prove that ∠C=60∘
Video Solution
Text Solution
Let D be the midpoint of the hypotenuse AC.
Join BD.
We have
AC2=AB2+BC2 [ by Pythagoras theorem]
⇒AC2=(√3BC)2+BC2[∴AB=√3BCgiven]
⇒AC2=4BC2⇒AC=2BC
⇒2CD=2BC[∴D is the midpoint of AC]
⇒CD=BC...(i)
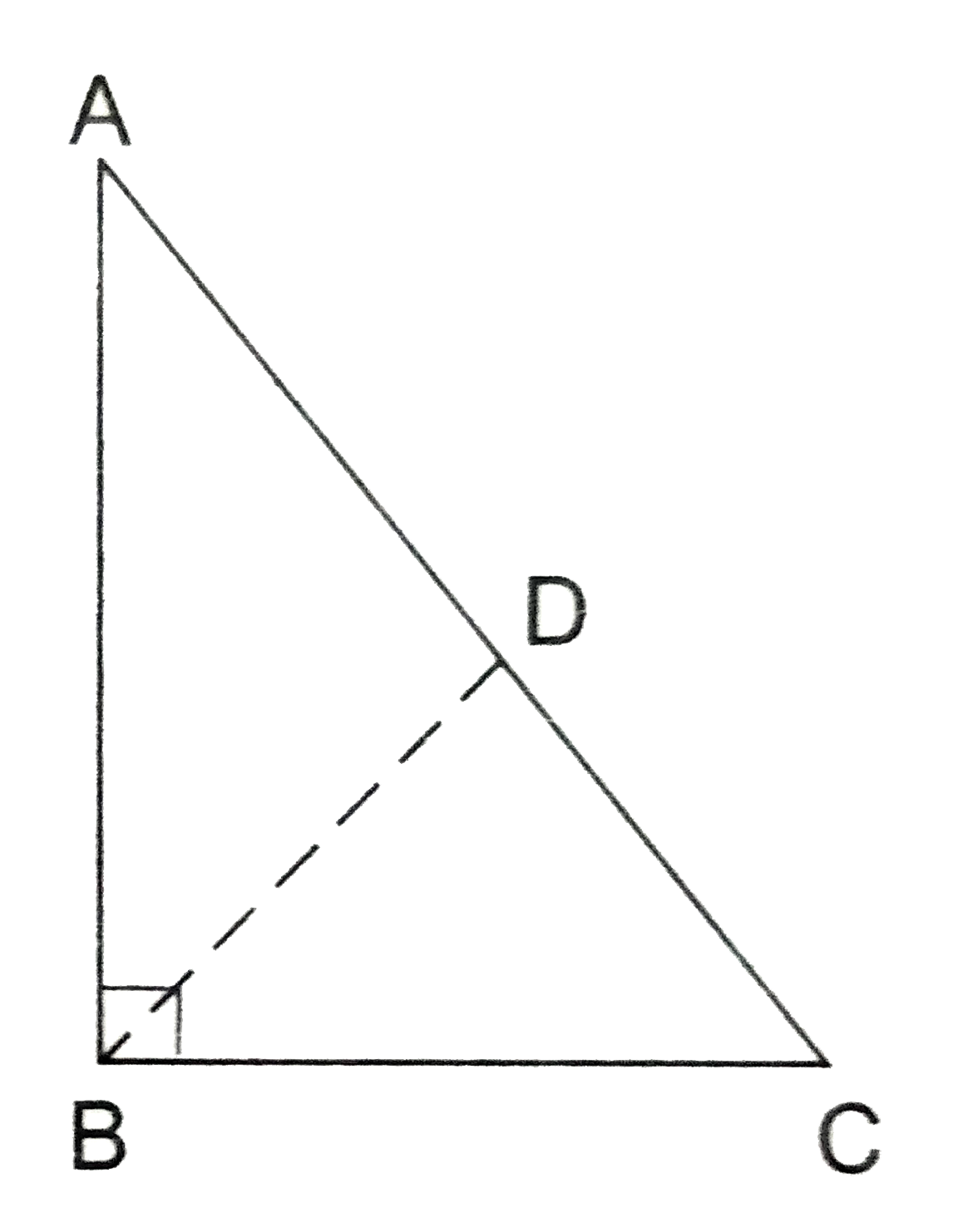
Also, we know tha the midpoint of the hypotenus of a right triangle is equidistant from the vertices
∴BD=CD ....(ii)
From (i) and (ii), we get
BC=BD=CD
∴ΔBCD is equilateral and hence ∠C=60∘
|
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Knowledge Check
In ΔABC, if ∠A=60∘,∠B=50∘,and∠C=70∘, then find the longest side of the triangle ABC.
ABCBABCACDNone of these
ABC is a right triangle right-angled at CandAC=√3BC . Prove that ∠ABC=600.
View SolutionIn ΔABC,∠B=90∘ and d is the mid - point of BC. Prove that AC2=AD2+3CD2
View SolutionABC is a right angled triangle in which ∠B=90∘andAB=BC. Find ∠Aand∠C.
View SolutionIn the given figure, in ΔABC,∠B=∠CandBD=CE. Prove that DE∣∣BC.

View SolutionIn a ΔABC∠C=60∘∠B=90∘ find the ratio of sides
View Solutionin triangle ABC angle C is 90∘,a=3,b=4 and D is point on AB so that angle BCD=30∘ then find length of CD
View SolutionIf in a ΔABC,b=√3,c=1andB−C=90∘, then ∠A is
View Solution
