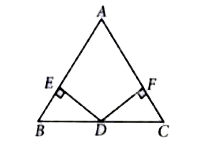
In an equilateral triagnle ABC, if AD bot BC then which of the follo

In an equilateral $Δ A B C$ if $A D ⊥ B C$ , then
A $2 A B^{2} = 3 A D^{2}$
B $3 A B^{2} = 4 A D^{2}$
C $5 A B^{2} = 6 A D^{2}$
D $4 A B^{2} = 5 A D^{2}$
In the given figure, AB = BC, AD = CD. Then, which of the following is true?

A $∠ A D E = 90^{\circ}$
B $A E = E C$
CBoth (a) and (b)
DAE=BC
In a $△ A B C$ ,AB = AC and $A D ⊥ B C$ , then :
A $A B < A D$
B $A B > A D$
CAB=AD
D $A B \leq A D$

In an equilateral triangle ABC, if $A D ⊥ B C$ then which of the following is true?