A rope of negligible mass can support a load of M kg. What will be the mass of the greatest load raised by the rope? Where g is the acceleration due to gravity and h is the height through which the said load rises from rest with uniform acceleration in time t.
M1+2hgt2kg
M2hgt2kg
Mgt22h−gt2kg
Mh22h+gt2kg
The correct Answer is:A
To solve the problem, we need to find the maximum mass m that can be raised by a rope supporting a load M kg, given that the load rises to a height h with uniform acceleration in time t.
1. Understand the Forces Acting on the Mass:
- The mass m is being lifted by the tension T′ in the rope.
- The weight of the mass m acting downwards is mg.
- The tension T′ must overcome this weight and provide the necessary upward acceleration.
2. Apply Newton's Second Law:
- The net force acting on the mass m can be expressed as:
T′−mg=ma
- Rearranging gives us:
T′=mg+ma
3. Express the Tension in Terms of Maximum Load:
- The maximum tension T that the rope can support is equal to the weight of the load M:
T=Mg
- Therefore, we can set T′ equal to T for the maximum load condition:
Mg=mg+ma
4. Solve for the Maximum Mass m:
- Rearranging the equation gives:
Mg=m(g+a)
- Thus, the maximum mass m can be expressed as:
m=Mgg+a
5. Determine the Acceleration a:
- To find a, we can use the second equation of motion:
h=ut+12at2
- Since the initial velocity u=0:
h=12at2
- Rearranging gives:
a=2ht2
6. Substitute a Back into the Equation for m:
- Substitute a into the expression for m:
m=Mgg+2ht2
- This can be simplified to:
m=Mgg+2ht2=Mgt2gt2+2h
Final Expression for Maximum Mass m:
Thus, the maximum mass m that can be raised by the rope is:
m=Mgt2gt2+2h
- The mass m is being lifted by the tension T′ in the rope.
- The weight of the mass m acting downwards is mg.
- The tension T′ must overcome this weight and provide the necessary upward acceleration.
- The net force acting on the mass m can be expressed as:
T′−mg=ma
- Rearranging gives us:
T′=mg+ma
- The maximum tension T that the rope can support is equal to the weight of the load M:
T=Mg
- Therefore, we can set T′ equal to T for the maximum load condition:
Mg=mg+ma
- Rearranging the equation gives:
Mg=m(g+a)
- Thus, the maximum mass m can be expressed as:
m=Mgg+a
- To find a, we can use the second equation of motion:
h=ut+12at2
- Since the initial velocity u=0:
h=12at2
- Rearranging gives:
a=2ht2
- Substitute a into the expression for m:
m=Mgg+2ht2
- This can be simplified to:
m=Mgg+2ht2=Mgt2gt2+2h
Thus, the maximum mass m that can be raised by the rope is:
m=Mgt2gt2+2h
Topper's Solved these Questions
- LAWS OF MOTION BOOK - MTG-WBJEECHAPTER - LAWS OF MOTION EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (CATEROGY 1: SINGLE OPTION CORRECT TYPE (1 MARK))
10 Videos
- LAWS OF MOTION BOOK - MTG-WBJEECHAPTER - LAWS OF MOTION EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 2: SINGLE OPTION CORRECT TYPE (2 MARKS))
1 Videos
- LAWS OF MOTION BOOK - MTG-WBJEECHAPTER - LAWS OF MOTION EXERCISE - WB JEE WORKOUT (CATEGORY 2: SINGLE OPTION CORRECT TYPE (2 MARKS))
15 Videos
- KINETIC THEORY OF GASES BOOK - MTG-WBJEECHAPTER - KINETIC THEORY OF GASES EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (MCQ)
7 Videos
- MAGNETIC EFFECT OF CURRENTBOOK - MTG-WBJEECHAPTER - MAGNETIC EFFECT OF CURRENTEXERCISE - WB JEE Previous Years Questions
22 Videos
Similar Questions
A rope of negligible mass can support a load of M kg. Prove that the mass of the greatest load which can be raised is equal to M1+2hgt2kg, where g is the acceleration due to gravity and h is the height through which the said load rises from rest with uniform acceleration in time t.
View SolutionA work of 4900 J is done on a load of mass 50 kg to lift it to a certain height. What is the height through which the load is lifted ?
View Solution
Knowledge Check
What will be the acceleration due to gravity at height h<<R . Where R is radius of earth and g is acceleration to gravity on the surface earth
Ag(1+hR)2Bg(1−2hR)Cg(1−hR)2Dg(1−hR)What will be the acceleration due to gravity at height h if h gt gt R . Where R is radius of earth and g is acceleration due to gravity on the surface of earth
Ag(1+hR)2Bg(1−2hR)Cg(1−hR)2Dg(1−hR)USS 150) Two masses of 5 kg and 10 kg are connected to a pulley as shown. What will be the acceleration of the system (g= acceleration due to gravity)
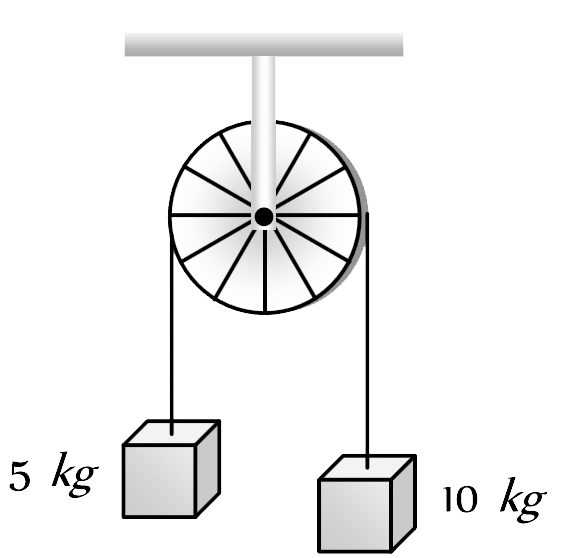 AgBg4C4g9D5g9
AgBg4C4g9D5g9
A rope of negligible mass is wound around a hollow cylinder of mass 3kg and radius 40cm. What is the angular acceleration of the cylinder, if the rope is pulled with a force of 30N ? What is the linear acceleration of the rope ? Assume that there is no slipping.
View SolutionA 40 kg boy climbs a rope that passes over an ideal pulley. The other end of the rope is attached to a 60 kg weight placed on the ground. What is the maximum upward acceleration the boy can have without lifting the weight ? If he climbs the rope with upward acceleration 2 g, with what acceleration the weight will rise up ?
View SolutionA particle of mass 'm' is raised to a height h=R from the surface of earth. Find increase in potential energy. R= radius of earth. g= acceleration due to gravity on the surface of earth.
View SolutionA simple pendulum with a bob of mass m oscillates from A to C and back to A such that PB is H. If the acceleration due to gravity is g, then the velocity of the bob as it passes through B is
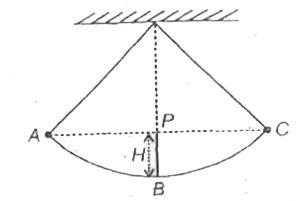
View SolutionA body of mass m rises to a height h=R/5 from the surface of earth. If g is the acceleration due to gravity at the surface of earth, the increase in potential energy is (R = radius of earth)
View Solution
