Two ships are 10√2 km apart on a line running south to north. The one further north is moving west with a speed of 25 km/h, while the other towards north with a speed of 25 km/h.
Their distance of closest approach is 5√2 km.
Their distance of closest approach is 10 km
Time required to reach the closest distance is 17 min
Time required to reach the closest distance is 29 min.
The correct Answer is:B, C
To solve the problem, we need to determine the distance of closest approach between the two ships and the time taken to reach that distance. Let's break it down step by step.
Step 1: Understand the Initial Setup
- We have two ships, A and B.
- Ship A is moving west at a speed of 25 km/h.
- Ship B is moving north at a speed of 25 km/h.
- The initial distance between the two ships is 10√2 km.
Step 2: Visualize the Motion
- Ship A is moving horizontally (west), while Ship B is moving vertically (north).
- The initial distance between them forms a right triangle where:
- One leg is the distance Ship A is moving west.
- The other leg is the distance Ship B is moving north.
Step 3: Relative Velocity
To find the distance of closest approach, we need to calculate the relative velocity of Ship B with respect to Ship A.
- The speed of Ship A (moving west) is VA=25 km/h.
- The speed of Ship B (moving north) is VB=25 km/h.
Since the two velocities are perpendicular to each other, we can use the Pythagorean theorem to find the relative speed VBA of Ship B with respect to Ship A:
VBA=√V2A+V2B=√(25)2+(25)2=√625+625=√1250=25√2 km/h
Step 4: Finding the Distance of Closest Approach
The closest distance occurs when the line connecting the two ships is perpendicular to the direction of motion of either ship.
Using trigonometry, we can find the distance of closest approach D using the sine of the angle formed by the paths of the ships. The angle θ can be calculated as:
tanθ=VBVA=2525=1⇒θ=45∘
Using the sine function:
D=sin(45∘)×PQ
Where PQ is the initial distance between the ships:
D=1√2×10√2=10 km
Step 5: Calculate the Time to Reach Closest Distance
To find the time T taken to reach the closest distance, we can use the formula:
T=DistanceRelative Speed=PQ⋅cos(45∘)VBA
Substituting the values:
T=10√2⋅1√225√2=1025√2=1025√2⋅6060=60025√2=24√2 hours
Converting to minutes:
T=24×60√2≈17 minutes
Summary of Results
1. The distance of closest approach is 10 km.
2. The time required to reach the closest distance is approximately 17 minutes.
- We have two ships, A and B.
- Ship A is moving west at a speed of 25 km/h.
- Ship B is moving north at a speed of 25 km/h.
- The initial distance between the two ships is 10√2 km.
- Ship A is moving horizontally (west), while Ship B is moving vertically (north).
- The initial distance between them forms a right triangle where:
- One leg is the distance Ship A is moving west.
- The other leg is the distance Ship B is moving north.
To find the distance of closest approach, we need to calculate the relative velocity of Ship B with respect to Ship A.
- The speed of Ship B (moving north) is VB=25 km/h.
The closest distance occurs when the line connecting the two ships is perpendicular to the direction of motion of either ship.
To find the time T taken to reach the closest distance, we can use the formula:
1. The distance of closest approach is 10 km.
2. The time required to reach the closest distance is approximately 17 minutes.
Topper's Solved these Questions
- BOOK - MTG-WBJEECHAPTER - LAWS OF MOTION EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (CATEROGY 1: SINGLE OPTION CORRECT TYPE (1 MARK))10videos
LAWS OF MOTION
- BOOK - MTG-WBJEECHAPTER - LAWS OF MOTION EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 2: SINGLE OPTION CORRECT TYPE (2 MARKS))1videos
LAWS OF MOTION
- BOOK - MTG-WBJEECHAPTER - LAWS OF MOTION EXERCISE - WB JEE WORKOUT (CATEGORY 2: SINGLE OPTION CORRECT TYPE (2 MARKS))15videos
LAWS OF MOTION
- BOOK - MTG-WBJEECHAPTER - KINETIC THEORY OF GASES EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (MCQ)7videos
KINETIC THEORY OF GASES
- BOOK - MTG-WBJEECHAPTER - MAGNETIC EFFECT OF CURRENTEXERCISE - WB JEE Previous Years Questions22videos
MAGNETIC EFFECT OF CURRENT
Similar Questions
To ships 10 km apart on a line running south to north . The one father north is steaming west at 20 km/h. The other is steaming north at 20 km/h. The distance of closest approach is . . . . to reach it the time taken is . . . .
View SolutionTwo ships are 10km apart on a line joining south to north. The one farther north is steaming west at 20kmh−1. The other is steaming north at 20kmh−1. What their distance of closest approach ? How long do they take to reach itb ?
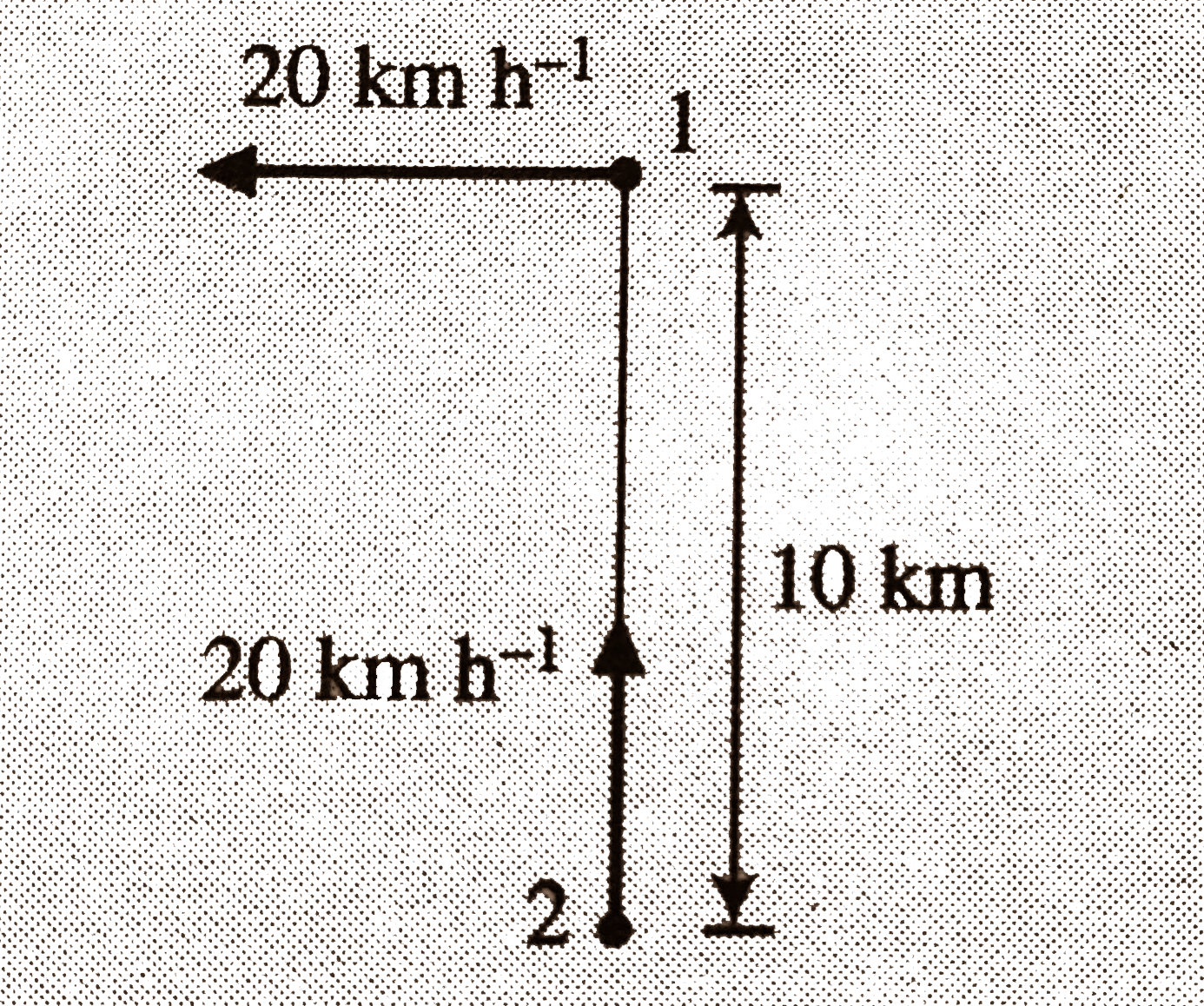 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One
Two ships are 10km apart on a line from south to north.The one farther north is moving towards west at 40kmph and the other is moving towards north at 40kmph.Then distance of their closest approach is
A10kmB10√2kmC10√2kmD20km - Question 2 - Select One
Two parallel rail tracks run north-south. On one track train A moves north with a speed of 54kmh−1 and on the other track train B moves south with a speed of 90kmh−1. The velocity of train A with respect to train B is
A10ms−1B15ms−1C25ms−1D40ms−1
Two ships A and B are 10km apart on a line running south to north. Ship A farther north is streaming west at 20km/h and ship B is streaming north at 20km/h. What is their distance of closest approach and how long do they take to reach it?
View SolutionA political party has to start its procession in an area where wind is blowing at a speed of 30√2kmh−1 and party flags on the cars are fluttering along north - east direction. If the procession starts with a speed of 40kmh−1 towards north, find the direction of flags on the cars.
View SolutionTwo ships move from a point at the same time. First ship moves at the speed of 24 km/hr at 45∘ angle from north to east and second ship moves at the speed of 32 km/hr at 75∘ angle from south to east. Find the distance between them after 3 hours.
View SolutionA plane is to fly due north. The speed of the plane relative to the air is 200 km/h, and the wind is blowing from west to east at 90 km/h.
View SolutionFrom a light-house an observer two ships A and B. Ship A proceeding towards north at a speed 20√2km/h and ship B proceeding towards north-east at a speed of 20km/h. Find in which direction and at what speed the ship B would appear to move to an observer standing on the deck of the ship A.
View SolutionTwo paarallel rail tracks run north-south Train A moves north with a speed of 54kmh−1 and train B moves south with a speed of 90kmh−1. What is the
a. relative velocity of B with respect to A?
b. relaity of a monkey running on the roof of the train A against its motion (with its velocity of 18kmh1 with respect ot the train A ) as observed by a man standing on the fround?View Solution

