8. Let S, be a square of unit area. A circle C1, is inscribed in S1, a square S2, is inscribed in C1 and so on. In general, a circle Cn is inscribed in the square Sn, and then a square Sn+1 is inscribed in the circle Cn. Let an denote the sum of the areas of the circle C1,C2,C3,.....,Cn then limn→∞an must be
Step by step video & image solution for 8. Let S, be a square of unit area. A circle C_1, is inscribed in S_1, a square S_2, is inscribed in C_1 and so on. In general, a circle C_n is inscribed in the square S_n, and then a square S_(n+1 is inscribed in the circle C_n. Let a_n denote the sum of the areas of the circle C_1,C_2,C_3,.....,C_n then lim_(n->oo) a_n must be by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A square is inscribed in circle of radius R, a circle is inscribed in the square, a new square in the circle and so on for n times.
Sum of the areas of all circles is
View SolutionA square is inscribed in a circle of radius R, a circle is inscribed in this square then a square in this circle and so on n times. Find the limit of the sum of areas of all the squares as n→∞.
View Solution
Knowledge Check
A square is inscribed in circle of radius R, a circle is inscribed in the square, a new square in the circle and so on for n times.
Sum of the areas of all circles isA4πR2(1−(12)n)B2πR2(1−(12)n)C3πR2(1−(13)n)DπR2(1−(12)n)A square is inscribed in a circle then another circle is inscribed in the square . Another square is then inscribed in the circle. Finally a circle is inscirbed in the innermost square . Thus there are 3 circles and 2 squares as shown in the figure . The radius of the outer - most circle is R .
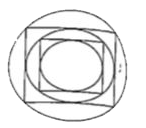
What is the sum of areas of all the squares shown in the figure ?A3R2B3√2R2C3√2R2Dnone of these
A square is inscribed in a circle of radius R, a circle is inscribed in this square then a square in this circle and so on n times. Find the limit of the sum of areas of all the squares as n→∞.
View SolutionLet circle c1, be inscribed in a square with side length 1. As shown in figure smaller circle c1 is inscribed in the lower right corner of the square so that c1 is tangent to c2 and the two sides of the square then the area of the c2 is
View SolutionLet circle 'c1' be inscribed in a square whith side lenght 1. As shown in figure smallar cicle c2 is inscribed in the lower right corner of the square so that c2 is tangent to 'c_1'andthetwossofthe□thentheareaofthe'c_2' is
View SolutionA square circumscribes a circle and another square is inscribed in this circle with one vertex at the point of contact. The ratio of the areas of the circumscribed and the inscribed squares is (a) 1 (b) 2 : 1 (c) 3 (d) 4
View SolutionFind the area of the circle in which a square of area 64 cm2 is inscribed. [Use π=3.14]
View SolutionFind the area of the circle in which a square of area 64 cm2 is inscribed. [Use π=3.14]
View Solution
